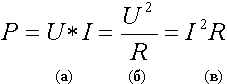|
| О нас | Услуги | Оборудование | Книги по теме | Примеры | Связь | Карта | Форум | Видео | En |
II. ОБ ИСТОЧНИКАХ ИНФОРМАЦИИ ПРИ ИЗУЧЕНИИ ПОЛЯ УПРУГИХ КОЛЕБАНИЙ О наличии или отсутствии упругих колебательных процессов можно узнать при наличии соответствующего датчика. В простейшем случае, при регистрации звуковых колебаний в воздухе таким датчиком может служить ухо, но такая информация имеет субъективный характер. Для получения объективной информации о параметрах регистрируемых колебательных процессов в этом простейшем случае используют микрофон с последующими измерениями параметров снимаемого с него электрического сигнала.
где V - скорость распространения упругих волн; |
II.1. Спектрально-временные представления Практика акустических измерений и сейсморазведочных исследований такова, что сигналы обычно изучаются во временнóм виде, то есть когда по оси абсцисс при изображении сигнала откладывают время, а по оси ординат - амплитуду. Однако ограничиться таким изображением было бы возможно только в том случае, если бы структура сигналов действительно, как и предписывается традиционным подходом, обуславливалась исключительно процессами отражений зондирующего сигнала от границ исследуемого объекта и интерференцией между этими отражениями. На самом же деле, как показали исследования (которые, кстати, и легли в основу настоящей работы), акустические и сейсмосигналы в основном обусловлены не интерференцией между элементарными отражениями, а наличием собственных колебательных процессов. Это различие принципиальное, но чтобы его увидеть, а главное, использовать для повышения эффективности интерпретации измерений, как раз и необходимо изучать сигналы не только во временнóм, но и в спектральном изображении, когда по оси абсцисс откладывают частоту, а по оси ординат - плотность спектра.
где F(t) - временнóе описание сигнала; A
Преобразования F(t) |
II.1.1. Синусоидальный сигнал
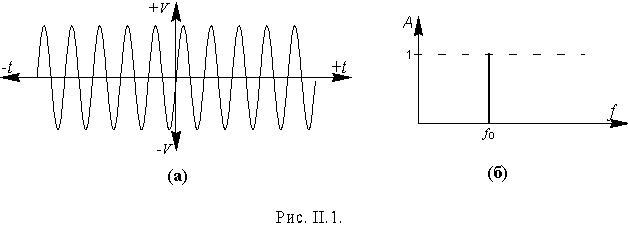
Электрическое напряжение в случае синусоидального сигнала изменяется по закону:
Изображение синусоиды на оси времени приведено на рис. II.1а. Понятно, что полностью временное изображение описать такой сигнал не может, поскольку длительность идеальной синусоиды бесконечна. Спектральное изображение синусоиды приведено на рис. II. 1б. Оно представляет собой отрезок вертикальной линии, проходящей через частоту f0 синусоидального процесса. Длина этого отрезка соответствует единице плотности спектра. Плотность спектра - функция вероятностная, и в данной ситуации это следует понимать таким образом, что в случае синусоиды вероятность обнаружения сигнала на частотной оси равна нулю на всех частотах, кроме частоты f0, а на этой частоте вероятность обнаружения сигнала равна единице.
|
II.1.2. Затухающий гармонический сигнал
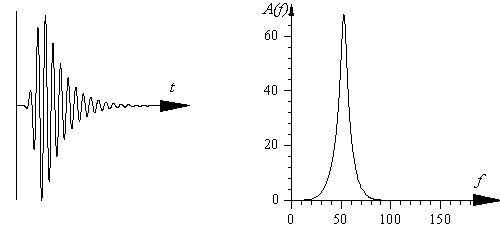
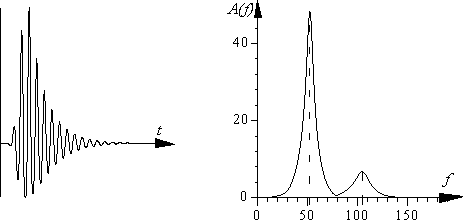
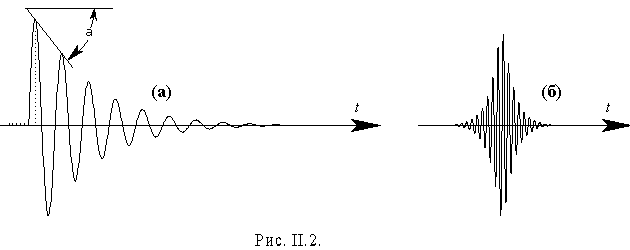
Два варианта затухающего синусоидального сигнала во временном изображении показаны на рис. II.2. Сигнал, изображенный на рис. II.2а, описывается следующим выражением:
где
где
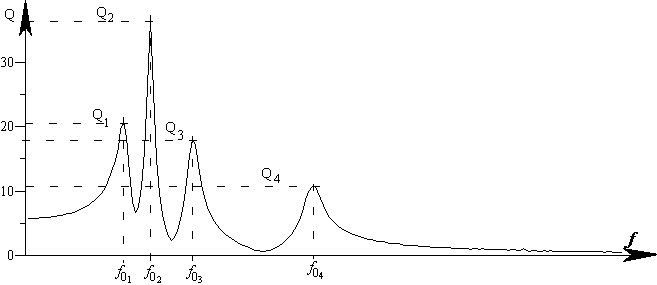
На рис. II.3 показаны спектральные изображения этих затухающих сигналов. Ось ординат проградуирована в значениях плотности спектра А. Значение плотности спектра на частоте f0 в дальнейшем будем воспринимать как добротность.
1Разумеется, с помощью цифрового синтеза может быть получен какой угодно сигнал, но это к нашему предмету не относится. |
II.1.3. Историческая справка Первый электрический колебательный контур был создан в 40-х годах прошлого века Джозефом Генри (тем самым, чье имя носит единица индуктивности). Это произошло случайно, при исследовании разряда конденсатора. Генри исследовал разряд заряженного конденсатора путем его короткого замыкания. На самом деле, это было не коротким замыканием, а разрядом через катушку индуктивности, поскольку для индикации тока разряда использовался прародитель современного амперметра, который представлял собой магнитную стрелку, окруженную большим количеством витков провода. Однако Дж. Генри считал провод достаточно толстым, чтобы пренебречь его сопротивлением, а действие индуктивного сопротивления было еще неизвестным.
где С - статическая емкость лейденской банки, а А - ее динамическая емкость.
|
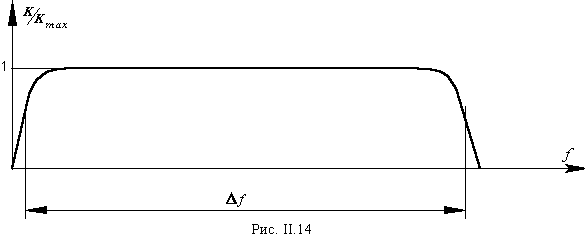
II.1.4. Об общих принципах регистрации колебательных процессов Установление через параметры сигнала факта наличия колебательных систем в изучаемых с помощью поля упругих колебаний объектах накладывает дополнительные требования к применяемым акустоэлектрическим преобразователям и ко всему тракту обработки сигналов. Требования эти заключаются в том, что акустоэлектрические преобразователи не должны искажать частотный спектр сигналов, полученных при исследовании различных объектов. Достигнуть это можно выполнением условия, которое заключается в том, что схемы регистрации и обработки сигнала не должны иметь собственной колебательности. Или, иначе говоря, не должны характеризоваться собственными частотами.
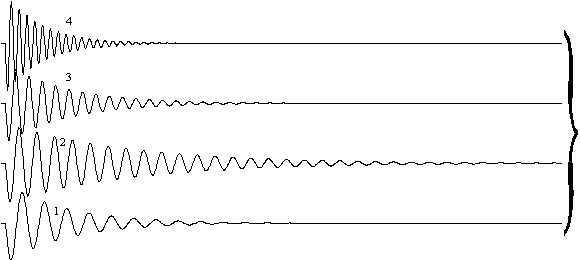
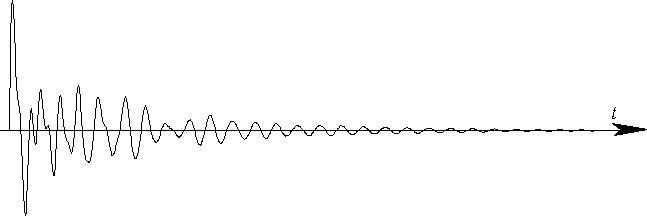
Суммированием этих четырех составляющих получен сигнал (б), очертания которого изменяются при любых изменениях фазовых соотношений между его составляющими.
Спектральное же изображение суммарного сигнала (в) содержит информацию о собственных частотах f0i возбуждаемых систем, а также о их добротностях, и от изменения фазовых соотношений между его составляющими не зависит.
|
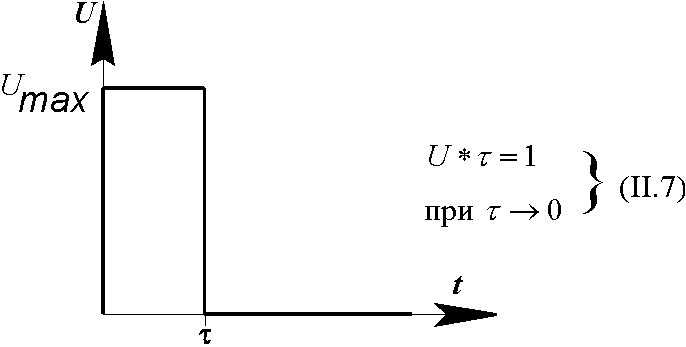
II.1.5. Импульсные сигналы Рассмотрение импульсных сигналов для нас важно потому, что находящиеся в большинстве твердых (а при некоторых условиях, и в жидких и газообразных) объектов колебательные системы, как и всякие колебательные системы, являются механизмами, преобразующими в гармонический затухающий отклик импульсное воздействие. При этом параметры отклика на импульсное воздействие определяются двумя взаимно независимыми факторами - свойствами возбуждаемых импульсным воздействием колебательных систем и параметрами самого импульсного воздействия.
То есть, иначе говоря,
В отличие от электрического, акустическое воздействие в виде прямоугольного импульса осуществить крайне сложно. Даже, более того, обычно не представляется возможным выяснить истинную форму импульсного воздействия. Однако независимо от формы импульса увеличение длительности ударного взаимодействия
Строго говоря, любое импульсное воздействие имеет бесконечный спектр. Выражение же (II.8) характеризует ту полосу частот |
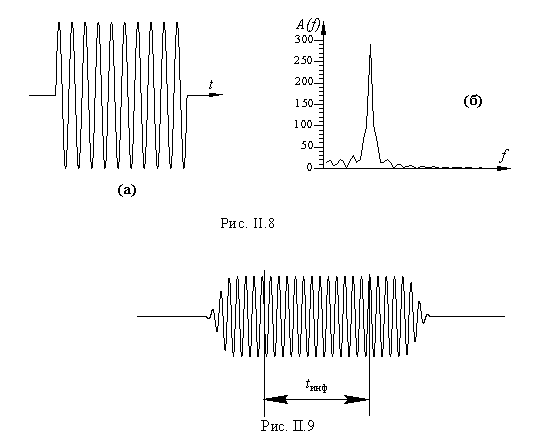
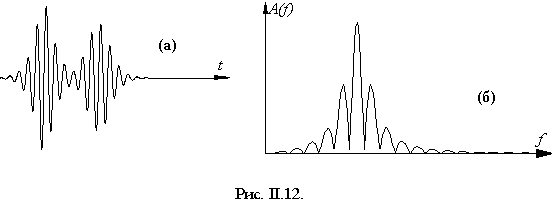
II.1.6. Радиоимпульс и импульсно-гармонический сигналРадиоимпульсом называют ограниченный во времени синусоидальный сигнал, временное изображение которого приведено на рис. II.8а. Импульсно-гармонический сигнал, изображенный на рис. II.9, отличается от радиоимпульса тем, что не имеет быстро изменяющихся по амплитуде (удароподобных) участков. Различие между этими сигналами очень существенно. Наличие удароподобных составляющих радиоимпульса приводит к тому, что он, по сути, не является узкополосным. И это понятно: резкий удар может возбудить колебательную систему в широком диапазоне частот. Наличие больших значений плотности спектра на спектральном изображении радиоимпульса в стороне от основной частоты (рис.II.8б) является тому доказательством.
Как известно, применение гармонического непрерывного сигнала при акустических измерениях крайне затруднительно, поскольку при этом нельзя разделить излученный и отраженный сигналы, а, кроме того, при этом возникают стоячие волны. Поэтому, согласно существующей методической литературе, для получения амплитудно-частотных акустических характеристик (АЧХ) различных объектов рекомендуется использовать в качестве зондирующего именно радиоимпульс. Однако в результате наблюдения его спектра должно быть ясно, что радиоимпульс не является узкополосным сигналом. Следовательно, он может оказаться причиной возникновения переходных процессов и возбудить колебательную систему с собственной частотой, в том числе и не совпадающей с частотой заполнения, и поэтому использовать радиоимпульс в качестве зондирующего сигнала для получения АЧХ при исследовании колебательных систем нельзя.
|
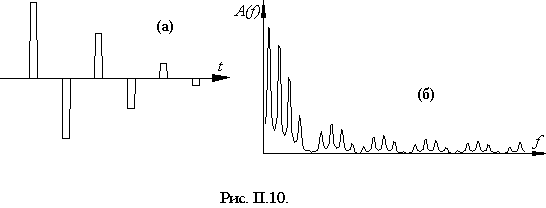
II.1.7. Многократно повторяющиеся сигналы Как утверждает теоретическая акустика, и это же лежит в основе традиционных сейсморазведочных методов, сигналы любых очертаний есть результат интерференции многократно повторяющихся одинаковых сигналов. В сейсморазведке при этом считается, что интерферируют между собой как бы элементарные эхо-сигналы, каждый из которых возникает за счет отражения зондирующего импульса от какой-то находящейся в земной толще неоднородности.
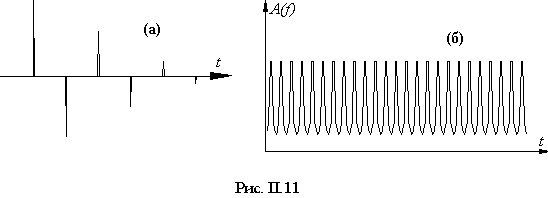
На рис. II.11а и б показано то же самое, но при малой длительности импульса.
Кто осуществляет практические сейсмоработы, знает, что подобного рода спектры не встречаются.
|
II.2. Принципы экспериментального наблюдения акустических и сейсмосигналов В общем случае, при проведении акустических измерений приходится применять устройство или систему устройств, структурная схема которых показана на рис. II.13.
При акустических измерениях информация, считываемая с регистрирующего устройства, формируется самим исследуемым объектом, акустоэлектрическим преобразователем и схемой обработки снимаемого с преобразователя электрического сигнала. На основании только лишь информации, считываемой с регистратора, без специальных исследований нельзя определить, как и какая именно составляющая схемы воздействовала на параметры исходного сигнала.
|
II.3. Свойства пьезоэлементов Использование прямого и обратного пьезоэффекта позволяет реализовать преобразователи как акустоэлектрические (аэп), так и электроакустические (эап). То есть с помощью аэп получать информацию в виде электрического сигнала о наличии сигнала акустического, а с помощью эап получать сигнал акустический путем электрического его возбуждения. Тот факт, что пьезопреобразователь является обратимой системой (то есть может быть одновременно и аэп и эап), дает возможность выявлять некоторые его параметры. В частности, наиболее существенную для нас, его АЧХ, а в конечном итоге, его колебательную характеристику.
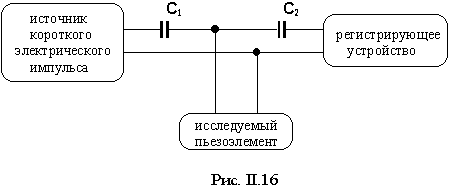
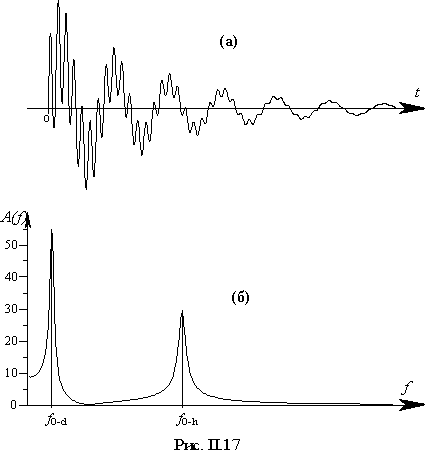
На рис. II.17 показано временнóе (а) и спектральное (б) изображение сигнала, полученного при использовании схемы, приведенной на рис.II.16. Исследуемый пьезоэлемент – пьезокерамический диск диаметром (d) 128 мм и толщиной (h) 19 мм. Материал – титанат бария. Два характерных экстремума на спектрограмме свидетельствуют о том, что пьезокерамический диск является колебательной системой с двумя собственными частотами. Наличие двух гармонических составляющих соответствует двум размерам объекта. То есть подобный пьезоэлемент является эквивалентом двум колебательным системам, собственная частота каждой из которых f0 связана с соответствующим размером так, что: по диаметру f0-d = 25 кГц;
Необходимо отметить, что начала обоих процессов не плавные, а удароподобные. Это имеет место потому, что электрическое возбуждение пьезокерамики подобно возбуждению механическому при совпадении формы фронта возбуждающего воздействия с формой соответствующей поверхности объекта.
Наличие выявленной таким образом собственной колебательности пьезокерамического диска свидетельствует о том, что подобный элемент не может быть использован в качестве аэп при спектрально-акустических измерениях.
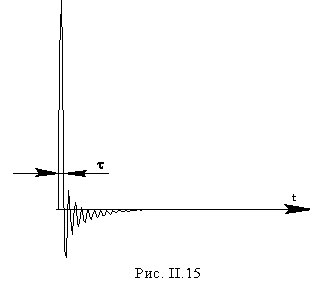
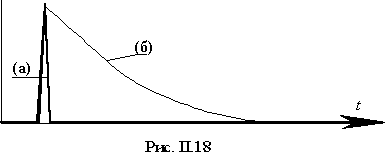
На временнóм изображении сигнала видно, что возбуждающий импульс (а), точно такой же, как использовался для возбуждения пьезокерамики, искажен только за счет емкостного характера электрического сопротивления пьезопленки. Об этом свидетельствует его длительный спад (б). Собственная же колебательность пьезопленки отсутствует.
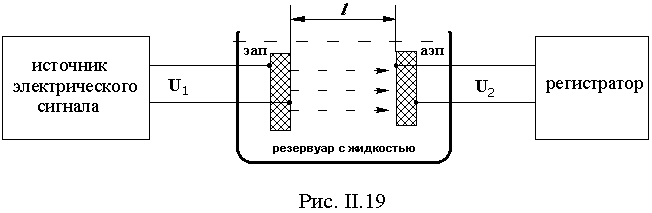
Оба преобразователя помещены в резервуар с звукопроводящей жидкостью (масло, вода) на расстоянии l друг от друга. Эта лабораторная установка представляется элементарно простой, однако без учета целого ряда факторов с ее помощью можно попасть в множество заблуждений.
|
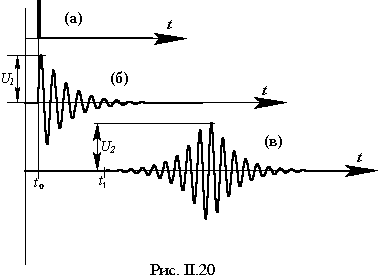
II.3.1. Основы ультразвуковых измерений Назначение ультразвуковых измерений - получать информацию о каких-то акустических свойствах прозвучиваемого объекта. Но для того, чтобы судить о свойствах объекта, необходимо сначала знать свойства самой измерительной установки. В наиболее общем и простейшем виде при измерениях скорости распространения поля упругих колебаний в качестве эап и аэп используются пьезокерамические диски с серебреными плоскими поверхностями, в качестве источника - генератор коротких импульсов, а регистратора - осциллограф. При этом обычно рекомендуется для повышения чувствительности установки (то есть увеличения отношения U2/U1) использовать совершенно одинаковые пьезокерамические диски с тем, чтобы они имели одинаковые собственные частоты. Насколько справедлива эта рекомендация, видно из рис. II.20, где показаны все преобразования сигнала по мере прохождения его от импульсного генератора до регистратора.
Но теперь возникает второй вопрос, а именно, как получить в точке U2 сигнал с удароподобным началом, подобный изображенному на рис. II.20б. Этого можно добиться двумя способами. Либо применить в качестве аэп пьезопленку, либо все же пьезокерамику, но таким образом, чтобы собственная частота ее была значительно выше, чем собственная частота эап. Для этого размеры (диаметр и толщина) аэп должны быть существенно меньше, чем размеры эап.
Относительная погрешность определения скорости при этом есть результат суммы относительной погрешности определения расстояния между преобразователями |
II. 4. Об измерениях энергетики Одной из наиболее разрабатываемых тем теоретической акустики являются вопросы, связанные с измерениями и оценкой энергетики поля упругих колебаний. Так, энергетику пытаются учитывать при регистрации подземных толчков, наблюдая импульсы акустической эмиссии, возникающие при разрушении горных пород при прессовых испытаниях и в условиях естественного залегания, и в ряде других случаев.
Или, в механике, при определении работы A, затрачиваемой на перемещение объекта, необходимо перемножить прикладываемую к объекту силу F на путь L, а оба эти линейные параметра должны быть определены непосредственным измерением.
|
II.5. Понятие о линейных и нелинейных процессах Нелинейность как физическая характеристика систем стала изучаться с развитием электротехники и радиотехники. Существенно нелинейные элементы - полупроводниковые и вакуумные приборы, а также компоненты, содержащие железо (трансформаторы и дроссели) используются для создания усилителей, генераторов и разного рода преобразователей спектра, само существование которых до изобретения нелинейных элементов было невозможным.
Затухающий гармонический сигнал, спектральное изображение которого содержит один экстремум (рис.II.21), проходя через существенно нелинейное звено, теряет свою симметричность относительно оси времени (рис.II.22), и на его спектральном изображении появляется дополнительный экстремум на частоте, вдвое большей частоты исходной, то есть на второй гармонике.
В зависимости от характера нелинейности схемы обработки сигнала (усилительного тракта) можно варьировать номерами гармоник и амплитудами сигнала на этих частотах, что широко использовалось в аналоговой радиотехнике. Таким образом, наличие нелинейности приводит не к появлению какого-либо колебательного процесса, а к формированию сигнала на гармониках исходного сигнала.
|
II.6. О типах упругих колебаний Понятия продольных и поперечных волн предложил Пуассон, в первой трети ХIХ века. Согласно кажущейся очевидной мысленной модели, носителями упругих колебаний являются минимально возможные частицы, из которых формируется материя. Модель эта предполагала следующую схему. При рассмотрении одномерной модели упругая продольная волна распространяется вдоль цепочки, состоящей из неких шариков (атомов) и пружинок между ними, роль которых выполняют межатомные взаимодействия. Цепочка, состоящая из последовательно соединенных масс и упругостей, является колебательной системой и обладает вполне конкретной собственной частотой. При частоте воздействия, превышающей эту частоту, упругое воздействие вдоль этой цепочки не распространяется. Расчеты, выполненные еще в начале ХХ века, показали, что частота эта не превышает одного мегагерца. И в учебниках, написанных до 30-х годов, утверждалось, что когда технические возможности акустики позволят достичь мегагерцовой части частотного диапазона, то мы все убедимся в том, что на этих частотах поле упругих колебаний распространяться в реальных средах не может.
|
II.7. О мнимости в физике Подходя к изучению процессов, связанных с возникновением собственных колебательных процессов, мы неизбежно должны столкнуться с понятием мнимости.
где j = Иначе выражение (II.10) можно представить следующим образом:
Абсцисса x и ордината jy совместно представляют собой комплексную плоскость и, соответственно, реальную (Real) и мнимую (Imreal) составляющие комплексной функции G.
где Z характеризует полное электросопротивление цепи, R - активная составляющая сопротивления цепи, а X - реактивная.
Забегая вперед, отметим, что гипотезы эти полностью подтверждаются. |
| Обсудить статью |
| При использовании материалов сайта ссылка на www.newgeophys.spb.ru обязательна | Публикации о нас |
|
|
|
|
|
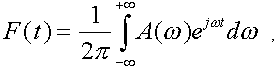 (II.2)
(II.2)
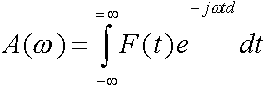 (II.3)
(II.3)
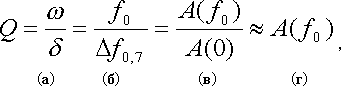 (II.6)
(II.6)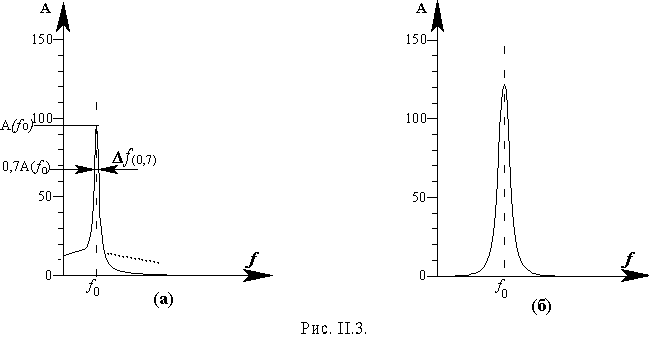
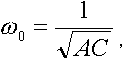
 Спектральное изображение
Спектральное изображение 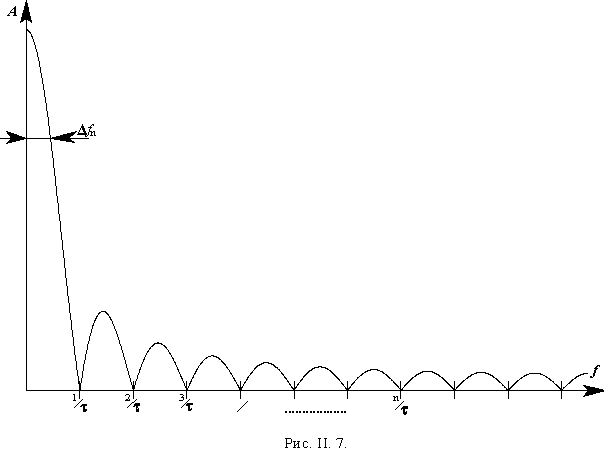
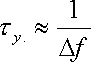 (II.8)
(II.8)

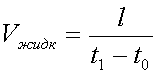 (II.9)
(II.9)