II.1.2. Затухающий гармонический сигнал
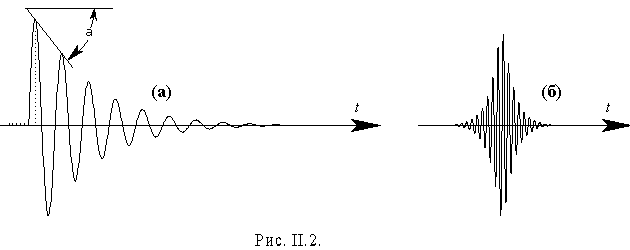
Два варианта затухающего синусоидального сигнала во временном изображении показаны на рис. II.2. Сигнал, изображенный на рис. II.2а, описывается следующим выражением:
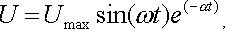 (II.5.)
(II.5.)
где  - коэффициент затухания:
- коэффициент затухания: 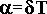 (T=1/f0);
(T=1/f0); 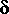 - коэффициент затухания, приведенный к периоду, и называемый декрементом затухания.
- коэффициент затухания, приведенный к периоду, и называемый декрементом затухания.
Затухающий синусоидальный сигнал характеризуется добротностью
Q, величина которой обратно пропорциональна затуханию. Если затухания нет, как в случае синусоидального незатухающего сигнала, добротность равна бесконечности. Другая крайность, это когда сигнал апериодический, и при этом
Q=1. Меньше единицы добротность быть не может.
Добротность может быть определена следующими способами:
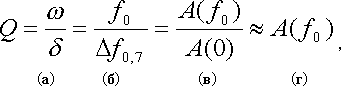 (II.6)
(II.6)
где 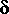 - декремент затухания затухающего синусоидального процесса;
- декремент затухания затухающего синусоидального процесса;
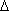 f0,7 - полоса пропускания колебательной системы;
f0,7 - полоса пропускания колебательной системы;
A(f0) и A(0) - плотности спектра соответственно на частоте f0 и на условно нулевой частоте.
Сигнал, изображенный на рис. II.2б, также является гармоническим затухающим, но, в отличие от изображенного на рис. II.2а, имеет плавным не только уменьшение, но и увеличение своей амплитуды.
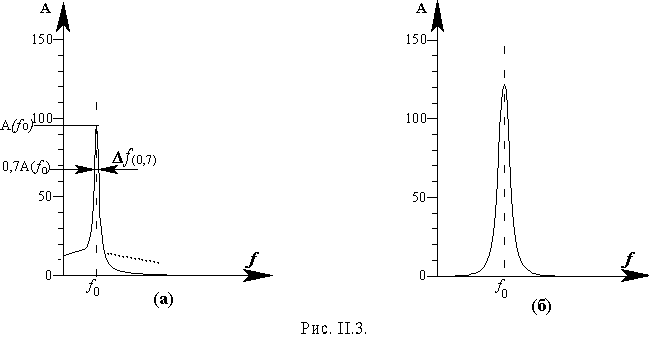
На рис. II.3 показаны спектральные изображения этих затухающих сигналов. Ось ординат проградуирована в значениях плотности спектра А. Значение плотности спектра на частоте f0 в дальнейшем будем воспринимать как добротность.
Строго говоря, затухающий синусоидальный сигнал гармоническим не является, и называют его почти периодическим или квазипериодическим. Однако по сути это ничего не меняет. Как и чисто синусоидальный, затухающий гармонический сигнал тоже не имеет гармоник, и так же точно не может быть получен путем интерференции более простых его составляющих. Получен такой сигнал тоже может быть только с помощью колебательной системы1, в результате ударного воздействия на эту систему.
Идеальной и наиболее изученной одночастотной колебательной системой является электрический L-C контур. Поэтому нам в дальнейшем удобно будет для рассмотрения физики упругих колебательных процессов привлекать аналогии со свойствами электрического колебательного контура. В соответствии с теорией и практикой колебательных контуров, спектральное изображение затухающего гармонического процесса, полученного при ударном воздействии на колебательный контур, оказывается эквивалентным амплитудно-частотной характеристике (АЧХ) этого контура. То есть различие в спектральном изображении сигналов, полученных при ударном воздействии на колебательные системы, обязательно соответствует различию их АЧХ.
Применительно к рис. II.3 можно сказать, что приведенные там очертания зависи-мо-стей амплитуды от частоты таковы, что, даже не зная, откуда они получены, можно сказать не колеблясь, что это либо спектральное изображение затухающего гармонического сигнала, либо амплитудно-частотная характеристика со-ответствующей колебательной системы. При этом совершенно несущественно, о какой именно колебательной системе идет речь - об электрическом контуре, механическом маятнике или даже просто о какой-то пока неизвестной колебательной системе.
Различие спектральных изображений обоих затухающих процессов, показанных на рис. II.3а и б обусловлено тем, что в процессе, изображенном на рис. II.3а, начало удароподобное, а в другом случае - плавно возрастающее по амплитуде. Но прежде, чем рассматривать причины этого различия, отметим еще и различие в добротностях Q обоих этих сигналов, несмотря на одинаковую скорость спада процесса в обоих случаях.
Дело в том, что добротность не является универсальным метрологически корректным параметром для оценки колебательных процессов. В реестрах метрологически узаконенных параметров добротность не значится. Как показало знакомство с научной литературой, этим словом характеризуют очень различные свойства субстанций в разных областях знания.
Строго говоря, параметром Q мы имеем право характеризовать только очень узкий класс колебательных процессов и, соответственно, колебательных систем. А именно, только единичные гармонические затухающие процессы с удароподобным началом. Обращаясь к аналогии с колебательным контуром, отметим, что такой сигнал возникает при ударном возбуждении контура с сосредоточенными параметрами. Сигнал, изображенный на рис. II.3б, может быть получен при ударном возбуждении контура с распределенными параметрами, и добротностью характеризоваться не может.
Однако, к сожалению, другого, более универсального параметра, чем добротность, для характеристики колебательных процессов пока не существует. Поэтому для оценки всех наблюдаемых нами колебательных процессов все же будем пользоваться, пусть и на чисто качественном уровне, добротностью Q. Наша многолетняя практика спектрально-акустических измерений вполне это допущение оправдывает, и использование этого параметра позволяет получать очень важную информацию, о чем речь также впереди.
Незатухающая синусоида имеет добротность, равную бесконечности, но при машинном преобразовании мы этого не увидим из-за характерных программных ограничений. Спектральное изображение синусоидального сигнала, полученное в результате аппаратурной реализации преобразования Фурье, прямую линию не даст. В случае аналогового спектроанализатора спектральное изображение синусоиды имеет вид, соответствующий амплитудно-частотной характеристике избирательного звена этой аппаратуры. Однако аналоговая аппаратура уходит в прошлое, и мы ее касаться не будем. Машинное (цифровое) спектральное изображение зависит как от количества точек на период синусоиды при оцифровке сигнала, так и от количества ее оцифрованных периодов. Для того чтобы вызванные этими ограничениями погрешности были меньше, необходимо увеличивать количество точек оцифровки на период исследуемого сигнала при увеличении общего количества точек. Это влечет за собой требование увеличения частоты дискретизации аналого-цифрового преобразователя и одновременно увеличения его памяти, и здесь каждый раз нужно находить компромисс, поскольку проблема переходит в экономический аспект. Что же касается минимального значения добротности, то при аппаратурном определении ее величина Q может быть и меньше единицы.
Для дальнейшего повествования очень важно уяснить, что наличие сигнала в виде гармонического затухающего процесса однозначно свидетельствует о том, что существует колебательная система, породившая его. Даже если нам неизвестна природа этой колебательной системы, это не должно быть основанием для того, чтобы усомниться в ее существовании.
Собственно говоря, именно эта позиция и положила начало всему направлению спектрально-акустических измерений. Возникающие в результате ударного воздействия на горный массив, а в общем случае, на большинство твердых объектов, затухающие гармонические процессы свидетельствуют о наличии в этих объектах колебательных систем.
1Разумеется, с помощью цифрового синтеза может быть получен какой угодно сигнал, но это к нашему предмету не относится.


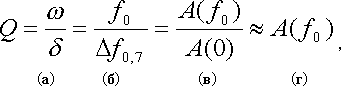 (II.6)
(II.6)