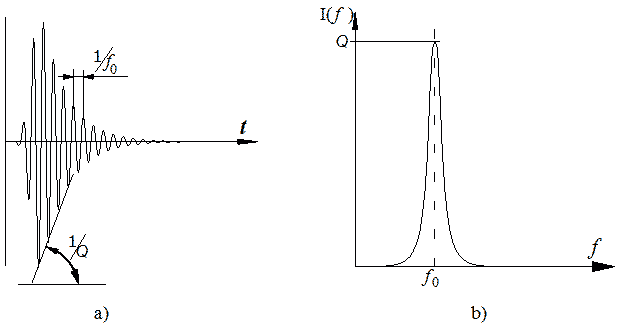
1.2. О спектральных характеристиках сигналов[1]

Дело в том, что такая вот, примерно колоколообразная¹ форма амплитудно-частотной характеристики есть не что иное как спектральное изображение затухающего синусоидального сигнала. Кроме того, как известно, подобную форму имеет амплитудно-частотная проходная характеристика одиночного электрического колебательного контура.

Зависимость между формой амплитудно-частотной характеристики тех или иных устройств и свойствами сигнала изучают в основах теоретической электротехники и теоретической радиотехники. Вкратце, то, что нас сейчас должно интересовать из этого, заключается в следующем.

Амплитудно-частотная характеристика колебательного контура по очертаниям совпадает с изображением частотного спектра сигнала, который возникает при ударном возбуждении этого колебательного контура. Для иллюстрации этого момента приведен рис.1-3, на котором изображена затухающая синусоида, которая возникает при ударном воздействии на колебательный контур. Этот сигнал приведен во временном (а) и спектральном (b) изображении.

Затухающая синусоида, которая возникает при ударном воздействии на колебательный контур
Рис. 1-3

Согласно разделу математики, называемому спектрально-времен-ными преобразованиями, спектральное и временное изображение одного и того же изменяющегося во времени процесса являются как бы синонимами, они эквивалентны и идентичны друг другу. Это можно сравнить с переводом одного и того же понятия с одного языка на другой. Любой человек, знакомый с этим разделом математики, скажет, что рисунки 1-3а и 1-3b эквивалентны друг другу. Кроме того, спектральное изображение этого сигнала, полученного при ударном возбуждении колебательной системы (колебательного контура) одновременно является геометрически подобным амплитудно-частотной характеристике этого самого контура.

Нетрудно заметить, что график (b) на рис.1-3 геометрически подобен графику 3 на рис.1-1. То есть, увидев, что в результате измерений был получен график 3, я сразу отнесся к нему не просто как к амплитудно-частотной характеристике затухания звука в породах кровли, но и как к свидетельству наличия в породной толще колебательной системы.

С одной стороны, наличие колебательных систем в горных породах, залегающих в кровле подземной выработки у меня не вызвало никаких вопросов, потому что другими способами получить синусоидальный (или, иначе говоря, гармонический) сигнал невозможно. С другой стороны, о наличии колебательных систем в земной толще я никогда раньше не слышал.

Для начала, напомним определение колебательной системы. Колебательная система - это объект, который на ударное (импульсное) воздействие реагирует затухающим гармоническим сигналом. Или, иначе говоря, это объект, обладающий механизмом преобразования импульса (удара) в синусоиду.

Параметры затухающего синусоидального сигнала - это частота f₀ и добротность Q, величина которой обратно пропорциональна коэффициенту затухания. Как видно из рис.1-3, оба эти параметра могут быть определены как из временного, так и из спектрального изображения этого сигнала.

Спектрально-временные преобразования - самостоятельный раздел математики, и один из выводов, который мы должны сделать из знания этого раздела, а также из формы амплитудно-частотной характеристики звукопроводности породного массива, изображенной на рис.1-1 (кривая 3), состоит в том, что по акустическим свойствам исследуемый породный массив проявил свойство колебательной системы.

Этот вывод является совершенно очевидным для любого, кто знаком со спектрально-временными преобразованиями, но категорически неприемлем для тех, кто профессионально занимается акустикой твердых сред, сейсморазведкой или вообще геофизикой. Так сложилось, что в курсе обучения студентов этих специальностей этот материал не дают.

Как известно, в сейсморазведке принято считать, что единственным механизмом, обуславливающим форму сейсмосигнала, является распространение поля упругих колебаний по законам геометрической оптики, отражение его от залегающих в земной толще границ и интерференция между отдельными составляющими сигнала. Считается, что форма сейсмосигналов обусловлена характером интерференции между множеством мелких эхо-сигналов, то есть отражений от множества мелких, залегающих в горном массиве границ. Кроме того, считается, что с помощью интерференции можно получить сигнал любой формы.

Да, это всё так, но в том-то и дело, что гармонический (в том числе, и гармонический затухающий) сигнал является исключением. Его интерференцией получить невозможно.

Синусоида - это элементарный информационный кирпичик, не подлежащий разложению на более простые составляющие, потому что проще, чем синусоида, сигнала в природе не существует. Именно поэтому, кстати, ряд Фурье - это совокупность именно синусоидальных членов. Будучи элементарным, неделимым информационным элементом, синусоида не может быть получена путем сложения (интерференции) каких бы то ни было других, еще более простых составляющих.

Получить гармонический сигнал можно одним-единственным путем - а именно, воздействием на колебательную систему. При ударном (импульсном) воздействии на колебательную систему возникает затухающая синусоида, а при периодическом или шумовом воздействии - незатухающая синусоида. А следовательно, увидев, что амплитудно-частотная характеристика некоего объекта геометрически подобна спектральному изображению гармонического затухающего сигнала, уже нельзя относиться к этому объекту иначе, как к колебательной системе.

Перед тем как проводить первые свои измерения в шахте, я, как и все остальные люди, функционирующие в области акустики твердых сред и сейсморазведки, был убежден, что никаких колебательных систем в породном массиве нет и быть не может. Однако обнаружив такую амплитудно-частотную характеристику затухания, я уже просто не имел права оставаться при этом мнении.

Проведение измерений, аналогичных описанным выше, весьма трудоемко, и обработка результатов этих измерений занимает много времени. Поэтому, увидев, что по характеру звукопроводности породный массив является колебательной системой, я понял, что следует использовать другую схему измерений, которую применяют при исследовании колебательных систем, и которую мы используем и по сей день. По этой схеме, источником зондирующего сигнала служит импульсное (ударное) воздействие на горный массив, а приемником - сейсмоприемник, специально предназначенный для проведения спектрально-сейсморазведочных измерений. Схема индикации и обработки сейсмосигнала позволяет наблюдать его как во временном, так и в спектральном виде.

Применив эту схему измерений в той же точке подземной выработки, что и при первом нашем измерении, мы убедились в том, что при ударном воздействии на породный массив кровли, сигнал, возникающий при этом, действительно имеет вид затухающей синусоиды, подобный показанному на рис.1-3a, а спектральное изображение ее подобно графику, показанному на рис.1-3b.

Чаще всего бывает, что сейсмосигнал содержит не одну, а несколько гармонических составляющих. Однако сколько бы ни было гармонических составляющих, они все возникают исключительно вследствие наличия соответствующего количества колебательных систем.

Многократные исследования сейсмосигналов, полученных в самых различных условиях - и в подземных выработках, и на земной поверхности, и в условиях осадочного чехла, и при исследовании пород кристаллического фундамента - показали, что во всех возможных случаях сигналов, полученных не в результате наличия колебательных систем, а в результате интерференционных процессов, не существует.

Строго говоря, форма спектра затухающего гармонического сигнала не совсем колоколообразная, но для нас сейчас эта неточность не имеет значения.