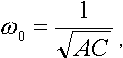ЧАСТЬ 1. ИСТОКИ

1. О наличии в сейсмосигнале гармонических затухающих процессов

1.1. О первых наших акустических измерениях в шахтных условиях

     Задача, поставленная передо мной при первом в моей жизни спуске в угольную шахту в 1977 году состояла в следующем. Нужно было необходимо найти технологичный и метрологически корректный способ определения затухания звука при распространении его в породах кровли. Это было необходимо для решения следующей задачи.
     Дело в том, что, согласно общепринятым представлениям, характер затухания звука в породах кровли должен быть как-то связан с их трещиноватостью, а следовательно, с вероятностью обрушения этих пород. И, стало быть, если осуществлять измерения, с помощью которых можно было бы оценивать это затухание, то можно было бы выйти на прогноз обрушения пород кровли в подземных выработках.
     Внезапное обрушение пород кровли - это очень грозное явление. Во всем Мире примерно половина травматизма подземных рабочих обусловлена именно этим явлением¹. Поэтому перед всеми научно-исследовательскими организациями горняцкого профиля обязательно стоит задача поиска признаков, с помощью которых стало бы возможным прогнозирование обрушения пород кровли. Поэтому перед всеми научно-исследовательскими организациями горняцкого профиля обязательно стоит задача поиска признаков, с помощью которых стало бы возможным прогнозирование обрушения пород кровли.
     В основе нашей попытки использовать акустические измерения для прогнозирования обрушения пород кровли лежали два казавшихся тогда очевидными положения. Первое заключается в том, что с удалением от источника сигнала амплитуда регистрируемого поля должна уменьшаться тем быстрее, чем более трещиноваты породы. И второе, которое состоит в том, что с увеличением частоты зондирующего сигнала интенсивность поля в точке приема должна уменьшаться также тем быстрее, чем более трещиноваты породы кровли.
     В соответствии с исходной идеей, чем выше трещиноватость пород кровли, тем выше вероятность их обрушения. И, стало быть, чем больше окажется затухание звука, распространяющегося в этих породах, тем ниже должна быть их устойчивость. То есть, следовало найти соответствие между зависимостями затухания звука от расстояния до источника для ряда фиксированных частот, и увязать эти зависимости с визуально наблюдаемой трещиноватостью пород кровли. И еще один момент из казавшихся очевидными. Чем выше трещиноватость пород кровли, тем больше должно быть затухание в высокочастотной части частотного диапазона зондирующего сигнала. И это также мы намеревались подтвердить экспериментальными зависимостями затухания от частоты.

Рис. 1-1

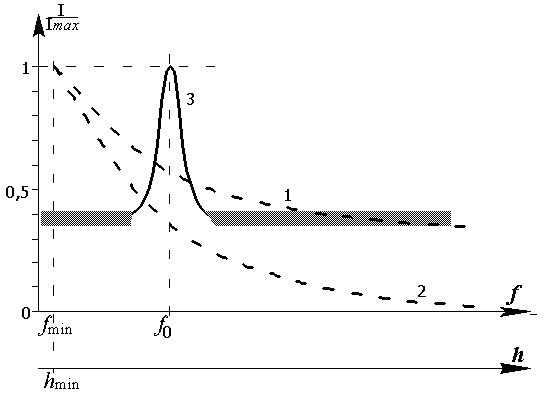
     Качественный характер этих обеих зависимостей затухания звука в породах кровли, какими они казались априорно, до проведения измерений, показан штриховыми кривыми 1 и 2 на рис.1-1. По оси ординат на этом рисунке откладывается относительная величина прохождения звука I в породах как величина, обратная затуханию; h - расстояние от источника звука; f - частота акустического сигнала. Предполагалось, что если проводить измерения в двух горных выработках с различной трещиноватостью кровли в них, то при переходе от пород кровли с меньшей трещиноватостью к породам с большей трещиноватостью зависимость 1 сменится на зависимость 2.
     При подготовке аппаратуры для реализации этой идеи возникло несколько непредвиденных проблем. Понятно, что универсальной аппаратуры не бывает, и для изготовления измерительной установки необходимо было иметь представление хотя бы о порядке ожидавшегося затухания, а также о том, что считать частотой низкой, а что - высокой. Кроме того, было непонятно, как решать проблему выбора электроакустического (излучателя) и акустоэлектрического (приемника) преобразователей для этой установки. Никаких конкретных рекомендаций в литературе не нашлось².
     Однако с чего-то нужно было начинать, и был собран (в шахтном исполнении, разумеется) генератор электрического напряжения изменяющейся частоты с диапазоном частот от 10 Гц до 20 кГц, и широкополосный усилитель с диапазоном входных напряжений - от 1мкВ до 1В и со стрелочным индикатором. В качестве излучателя и приемника были использованы одинаковые пьезокерамические преобразователи из стандартного комплекта гидроакустической измерительной аппаратуры. На рис.1-2 приведена блок-схема измерительной установки.

Рис. 1-2

     При проведении этих измерений неукоснительно выполнялось главное требование метрологии - оно заключается в том, что результаты должны быть повторяемы. Сразу отметим, что выполнить это требование для получения зависимости I(l) не удалось. При любом, самом незначительном перемещении измерительной установки, показания стрелочного индикатора отличались существенно больше, чем это можно было бы объяснить погрешностью аппаратуры. Причина этого явления стала понятной значительно позже, и описана она в разделе 6.
     И вот что при этом оказалось. При съемке зависимости затухания звука от частоты график I(f) оказался принципиально отличным от того, который ожидался, и имел вид графика 3, приведенного на рис.1-1, согласно которому, вместо того, чтобы уменьшаться с ростом частоты, амплитуда звука довольно резко увеличилась вблизи некоторой частоты f₀, а затем снизилась примерно до того же уровня. Вдали от частоты f₀ величина амплитуды, считываемая с индикатора усилителя, более или менее постоянна, что и показано на графике 3. При первом измерении частота f₀ имела значение, близкое к 1КГц.
     То, что с увеличением частоты затухание ощутимо не увеличивается, показалось очень странным. Ведь во всех учебниках по сейсморазведке утверждается, что верхний частотный предел сейсмостанций не превышает 1 КГц, поскольку на более высоких частотах уже практически никакого прохождения сигнала нет... Однако главным сюрпризом в этом эксперименте оказалась форма полученной кривой 3. Дело в том, что в такой форме амплитудно-частотной зависимости затухания звука, распространяющегося в горных породах, вблизи частоты f₀ заложен очень глубокий физический смысл.

---

¹ В России на травматизм от обрушения пород кровли приходится существенно меньший процент, так как основной травматизм у нас обусловлен невыполнением правил техники безопасности самими же рабочими.

² Я тогда просто еще не мог себе представить, что подобных измерений в акустике твердых сред просто никто никогда не делал.

1.2. О спектральных характеристиках сигналов

     Дело в том, что такая вот, примерно колоколообразная³ форма амплитудно-частотной характеристики есть не что иное как спектральное изображение затухающего синусоидального сигнала. Кроме того, подобную форму имеет амплитудно-частотная характеристика одиночного электрического колебательного контура.
     Физику связи между формой амплитудно-частотной характеристикой тех или иных устройств и свойствами того или иного сигнала изучает курс основ теоретической электротехники. Вкратце, то, что нас сейчас должно интересовать из этого курса, заключается в следующем.

Рис. 1-3

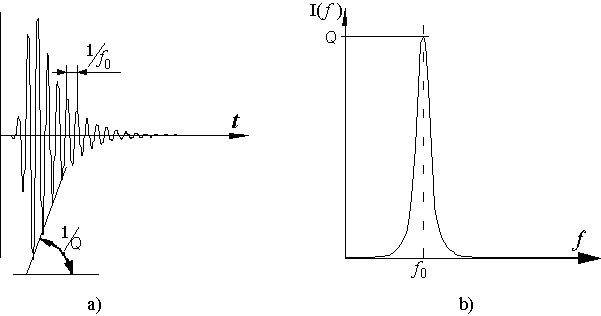
     Форма амплитудно-частотной характеристики колебательного контура идентична спектру сигнала, который возникает при ударном возбуждении этого колебательного контура. Для иллюстрации этого момента приведен рис.1-3, на котором изображена затухающая синусоида, которая возникает при ударном воздействии на колебательный контур. Этот сигнал приведен во временнóм (а) и спектральном (b) изображении.
     Спектральное и временнóе изображение одного и того же изменяющегося во времени процесса являются как бы синонимами, они эквивалентны и идентичны друг другу. Это как бы перевод одного и того же понятия с одного языка на другой. Кроме того, спектральное изображение этого сигнала, полученного при ударном возбуждении колебательной системы (колебательного контура) одновременно является и амплитудно-частотной характеристикой этого самого контура.
     Нетрудно заметить, что график (b) на рис.1-3 геометрически подобен графику 3 на рис.1-1. То есть, увидев, что в результате измерений получен график 3, я сразу отнесся к нему не только как к амплитудно-частотной характеристике затухания звука в породах кровли, но и как к свидетельству наличия затухающей синусоиды, которая должна возникнуть при ударном воздействии на эту кровлю. Что, кстати, затем, при использовании аппаратуры следующего поколения, и подтвердилось.
     Параметры затухающего синусоидального сигнала - это частота f₀ и добротность Q, величина которой обратно пропорциональна коэффициенту затухания. Как видно из рис.1-3, оба эти параметра могут быть определены как из временнóго, так и из спектрального изображения этого сигнала.
     Спектрально-временные преобразования - самостоятельный раздел математики, и один из выводов, который мы должны сделать из знания этого раздела, а также из того, что амплитудно-частотная характеристика звукопроводности породного массива, изображенная на рис.1-1 (кривая 3), имеет такую, как показано на рис.1-1 форму, состоит в том, что по акустическим свойствам исследуемый породный массив является колебательной системой. То есть обладает механизмом для преобразования удара в гармонический процесс.
     Этот вывод является совершенно очевидным для любого, кто знаком со спектрально-временными преобразованиями, но совершенно неприемлем для тех, кто профессионально занимается акустикой твердых сред или сейсморазведкой.
     Как известно, в сейсморазведке принято считать, что единственным механизмом, обуславливающим форму сейсмосигнала, является интерференция. Считается, что форма сейсмосигналов обусловлена характером интерференции между множеством мелких эхо-сигналов, то есть отражений от множества мелких, залегающих в горном массиве границ. Кроме того, считается, что с помощью интерференции можно получить сигнал любой формы.
     Но в том-то и дело, что гармонический (в том числе, и гармонический затухающий) сигнал интерференцией получить невозможно.
     Синусоида - это элементарный информационный кирпичик, не подлежащий разбиению на более простые составляющие. Именно поэтому ряд Фурье - это совокупность именно синусоидальных членов. Будучи элементарным, неделимым информационным элементом, синусоида не может быть получена путем сложения (интерференции) каких бы то ни было других, еще более простых составляющих. Потому что проще, чем синусоида, сигнала в природе не существует.
     Получить гармонический сигнал можно одним-единственным путем - а именно, воздействием на колебательную систему. При ударном (импульсном) воздействии на колебательную систему возникнет затухающая синусоида, а при периодическом воздействии – незатухающая синусоида. А следовательно, увидев, что амплитудно-частотная характеристика некоего объекта геометрически подобна спектральному изображению гармонического затухающего сигнала, уже нельзя относиться к этому объекту иначе, как к колебательной системе. Перед тем как проводить первые свои измерения в шахте, я был убежден, что никаких колебательных систем в породном массиве нет и быть не может. Однако обнаружив такую амплитудно-частотную характеристику затухания, я уже просто не мел права оставаться при этом мнении.
     Проведение измерений, аналогичных описанным выше, весьма трудоемко, и обработка результатов этих измерений занимает много времени. Поэтому, увидев, что по характеру звукопроводности породный массив является колебательной системой, мы применили другую схему измерений. Которую используем и по сей день. По этой схеме, источником зондирующего сигнала служит акустический импульс, возникающий в результате ударного воздействия на горный массив, приемником - сейсмоприемник, специально предназначенный для проведения спектрально-сейсморазведочных измерений. Схема обработки и индикации сейсмосигнала позволяет наблюдать его как во временнóм, так и в спектральном виде.
     Применив эту схему измерений в той же точке подземной выработки, что и при первом нашем измерении, мы убедились в том, что при ударном воздействии на породный массив кровли, сигнал, возникающий при этом, действительно имеет вид затухающей синусоиды, подобный показанному на рис.1-3a, а спектральное изображение ее подобно графику, показанному на рис.1-3b.
     Чаще всего бывает, что сейсмосигнал содержит не одну, а несколько гармонических составляющих. Однако сколько бы ни было гармонических составляющих, интерференционных составляющих в сейсмосигналах нет.
     Многократные исследования сейсмосигналов, полученных в самых различных условиях - и в подземных выработках, и на дневной поверхности, и в условиях осадочного чехла, и при исследовании пород кристаллического фундамента - показали, что практически во всех возможных случаях интерференционные составляющие сейсмосигнала отсутствуют.

---

³ Строго говоря, форма спектра затухающего гармонического сигнала не совсем колоколообразная, но для нас сейчас эта неточность не имеет значения.

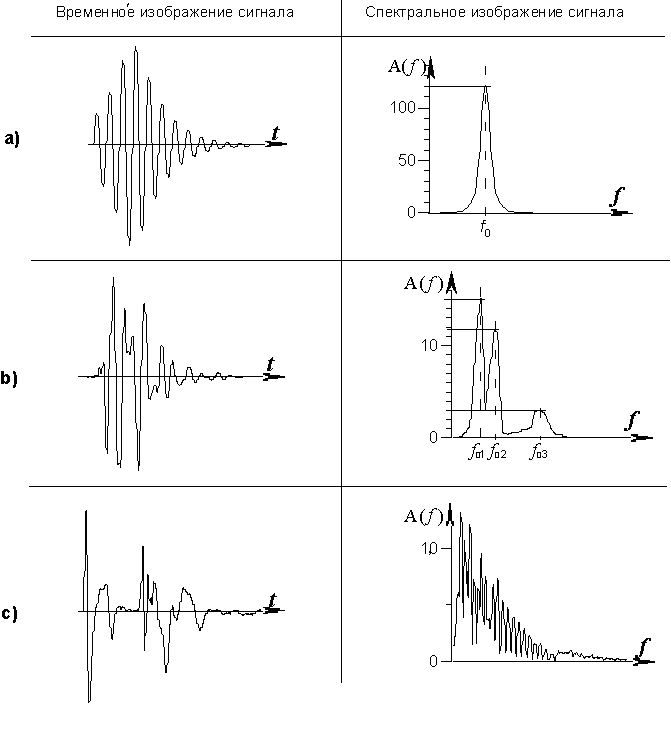
1.3. Как выявить наличие интерференционной составляющей сигнала

     Спектральное и временнóе изображения одного и того же сигнала информативно действительно полностью идентичны. Однако на практике в этом можно убедиться только в том случае, когда гармоническая составляющая всего одна. Если гармонических составляющих сигнала несколько, то выявить его структуру возможно только при его спектральном изображении. На рис.1-4 приведены три сигнала во временнóм и спектральном изображениях. Сигнал а) представляет собой одну затухающую синусоиду; в состав сигнала b) входят три затухающих синусоиды; сигнал с) возник в результате интерференции.

Рис. 1-4

     Оси ординат спектральных изображений размечены в значениях плотности спектра А(f), в соответствии с принятыми обозначениями при спектрально-временных преобразованиях. Добротность сигнала а) равна 120. Если для электрического колебательного контура такая добротность является средней по величине, то при сейсмоизмерениях - это очень высокое значение. Однако такое хоть и редко, но встречается. Такие случаи чреваты возникновением геодинамических явлений, о чем будет рассказано в разделе 13, во второй части настоящей работы.
     Сигнал b) - довольно типичный при сейсмоизмерениях. Он состоит из трех гармонических составляющих, каждая из которых имеет невысокие значения добротности - 15, 12 и 3. Это реальные, часто встречающиеся при сейсмоизмерениях значения добротности. На спектральном изображении нетрудно определить значения частот каждой из составляющих. Однако на временнóм изображении не то что определить параметры каждой колебательной системы, но даже понять, что сигнал состоит из трех гармонических составляющих - невозможно. Кроме того, очертания сигнала будут изменяться при изменении фазовых соотношений между этими составляющими. То есть любое перемещение измерительной установки при сейсмоизмерениях приведет к изменению очертаний сейсмосигнала.
     Вот это явление хорошо знакомо сейсморазведчикам - когда сейсмосигнал по форме изменяется при любом, самом незначительном изменении положения как точки ударного воздействия, так и местонахождения сейсмоприемников.
     Сигнал с) получен в результате интерференционного процесса. Как видим, на временн?м изображении существенного различия между сигналами b) и с) незаметно. Однако при спектральном их изображении разница между ними велика. Кроме того, что спектр интерференционного сигнала имеет характерный линейчатый характер, значение плотности спектра его не превышает единицы.
     Установить наличие гармонических составляющих в сейсмосигнале, а стало быть, наличие колебательных систем в породном массиве - это был очень непростой момент. Особенно когда весь научный мир категорически отрицает какие-либо механизмы формирования сейсмосигналов, кроме интерференционных. Однако установить наличие гармонических составляющих в сейсмосигнале - это был всего лишь первый шаг, и без дальнейших шагов сделанное заявление не имело бы особого смысла. Колебательная система характеризуется собственной частотой, и следующим шагом должно было быть установление зависимости между собственной частотой колебательной системы и какими-то ее конкретными физическими параметрами. Так сложилось, что этот второй шаг удалось сделать сразу же, при первом получении результатов шахтных сейсмоизмерений летом 1977 года, и описано это в разделе 2.

1.4. Исторический экскурс

     Совсем непросто было после очень многолетних утверждений о том, что все сейсмосигналы обусловлены интерференционными процессами, заявить, что это не так. Помогло мне сделать это знание истории открытия электрического колебательного контура.
     Открытие электрического контура происходило в 3 этапа.
     На первом этапе Джозеф Генри совершенно случайно обнаружил, что если заряженный конденсатор замкнуть накоротко, то происходит многократное изменение полярности тока разряда. Задачей эксперимента была попытка оценить энергетический баланс "электрической жидкости", как тогда называли эту субстанцию. Для этого Генри собрал устройство, которое потом получило название амперметра. Это была магнитная стрелка, окруженная большим количеством витков провода, достаточно толстого, чтобы можно было не считаться с его омическим сопротивлением. То есть, на самом деле, разряд конденсатора шел не накоротко, а через катушку индуктивности, и, стало быть, был реализован колебательный L-C контур. Но это мы уже сейчас понимаем, а тогда многократное изменение направления тока было объяснено "интерференционными процессами, которые возникают в результате короткого замыкания, поскольку это эквивалентно встряхиванию в лейденской банке (как тогда называли конденсатор) электрической жидкости. В результате этой интерференции электрическая жидкость не только выливается из лейденской банки, но и вливается обратно." В таком виде объяснение работы неосознанного колебательного контура существовало во всех учебниках и в научной литературе лет 30, пока этим не заинтересовался лорд Кельвин.
     Им был сделан второй шаг в открытии колебательного контура. Лорд Кельвин заинтересовался формой сигнала, который возникает при разряде конденсатора по описанной выше схеме. Чтобы удовлетворить свой научный интерес, он изобрел осциллограф, и увидел, что сигнал этот имеет форму затухающей синусоиды. И сразу во всеуслышание заявил об открытии неизвестной ранее колебательной системы, поскольку, в отличие от современных для нас с вами ученых, он ни секунды не сомневался, что создать синусоидальный сигнал можно только с помощью колебательной системы, и никак иначе. Поэтому лорд Кельвин сразу отверг интерференционную природу этого сигнала. Так что и мне ничего не оставалось другого как вслед за лордом Кельвином сказать, что если при ударном воздействии на горный массив возникает сигнал в виде затухающей синусоиды, значит, ударом мы возбудили какую-то колебательную систему.
     Здесь не тому следует удивляться, что я сделал заявление о наличии в горном массиве колебательных систем, а тому, что этого никто не сказал до меня. Ведь ряды Фурье изучают студенты всех технических учебных заведений. Но я думаю, что виновато здесь завораживающее воздействие слова "интерференция". Причем, не только в позапрошлом, XIX веке. Так, возьмем вполне современное радиотехническое устройство - СВЧ объемный резонатор. Это латунный стакан с серебреной внутренней поверхностью, поведение которого абсолютно идентично высокодобротному колебательному контуру. Так вот, работа объемного резонатора по сей день объясняется интерференционными процессами. Я не знаю механизма преобразования ударного воздействия в гармонический отклик в объемном СВЧ-резонаторе, но то, что он, безусловно, существует, и что интерференция здесь абсолютно ни при чем - сомнений вызывать не может.
     И, наконец, третий и окончательный этап в открытии электрического колебательного контура. Его осуществил лет через 10 после Кельвина, в 80-х годах XIX века, Фергюсон, написав работу о резонансных свойствах L-C цепей. Дело в том, что лорд Кельвин умудрился написать уравнение колебательного контура, все еще не подозревая ни о наличии, ни, тем более, о роли индуктивности. Уравнение, написанное Кельвиным, имело вид:

где С - статическая емкость конденсатора, а А - его динамическая емкость. И только в дальнейшем, уже после его смерти, A было заменено на индуктивность L. Сейчас, когда мы знаем физику работы электрического колебательного контура, любой школьник выведет его уравнение. Но вот как можно было вывести его, не зная даже о роли индуктивности - этого я не представляю себе.

1.5. О первом нашем измерении кинематических характеристик

     Первый результат, связанный с регистрацией собственных упругих колебаний в породных слоях, был получен при первом же моем спуске в шахту. Однако доклады об этом, которые мне приходилось делать в ходе выполнения научно-исследовательской работы, воспринимались в высшей степени отрицательно. Аргумент был странным, но я его слышал постоянно. Дескать, весь научный мир исследует кинематические характеристики поля упругих колебаний, и если спектр акустических сигналов никого не интересует, то и нам заниматься этим не следует.
     Поскольку я тогда читал курс шахтной геофизики, то в свете этих рекомендаций решил поставить лабораторную работу по физическому моделированию поля упругих колебаний в слоях (пластинах). А именно, решил предложить студентам осуществлять измерение скорости распространения звука в таких структурах.
     Но сначала о некоторых принципах определения скорости распространения упругих колебаний.

1.5.1. Об измерении скорости звука

     Измерение скорости звука - единственный вид акустических измерений, которые могут быть осуществлены на метрологически корректном уровне. Это определяется тем, что, применяя для измерений сейсмоприемник, мы достоверно только и можем, что определять момент, разделяющий отсутствие сигнала и его наличие. А основой определения⁴ скорости распространения (движения) любого объекта - это как раз и является процесс регистрации моментов прохождения этого объекта мимо точки регистрации. И вместе с тем, это единственно возможное из акустических измерений оказалось окружено таким количеством неопределенностей, запретов и условий, что этот вопрос просто необходимо рассмотреть подробнее.
     В волновое уравнение скорость распространения упругих колебаний входит как величина постоянная. Скорость распространения упругих колебаний в однородных по вещественному составу, монолитных средах - очевидно имеет постоянную величину, и в этом никто никогда не сомневался. Но вот чему равна эта величина - непонятно.
     С одной стороны, определение скорости - простейшая процедура. Регистрируем время пробега t исследуемой субстанции определенного промежутка (измерительной базы) l , и получаем значение скорости V, усредненное по величине l :

V = l / t        (1-1)

     Казалось бы, никаких проблем. Относительная погрешность результатов такого определения скорости получается простым сложением относительных погрешностей измерения отрезка пути l и измерения интервала времени t.
     Однако при подготовке лабораторных работ я обратил внимание на большое количество в научной литературе противоречий в определениях. И в первую очередь, на один очень интересный запрет. Почему-то условия допустимости определения скорости распространения с помощью выражения (1-1) связываются с соотношением между величиной l и длиной волны . И если, скажем, измерительная база l покажется кому-то недостаточно большой относительно длины волны, то результаты измерений могут быть опротестованы.
     На самом деле, этот запрет не имеет физического смысла. Дело в том, что если при измерениях происходит регистрация момента, разделяющего состояние наличия сигнала от состояния его отсутствия или, как обычно говорят, происходит регистрация момента первого вступления, то непонятно, причем тут длина волны. Ведь длина волны, которая, как известно, есть отношение скорости распространения конкретной субстанции к частоте ее изменения, может характеризовать только периодический процесс. Момент же первого вступления может аппроксимироваться функцией Хэвисайда (ступенька или скачок), которая не является периодическим процессом и длиной волны не характеризуется. Никакой моноимпульсный процесс не может характеризоваться длиной волны, а стало быть, не может длиной волны характеризоваться и ступенька.
     При определении скорости путем регистрации момента первого вступления выявляется самая большая скорость движения или, иначе говоря, скорость распространения фронта. Это аналогично тому, как когда бегун, пересекая линию финиша, рвет ленточку. Он рвет ее частью тела, которая первая пересекает линию финиша, и никого уже не интересует, сколько времени будут пересекать эту линию все оставшиеся там руки, ноги и т.д. Также и с акустическими измерениями, когда по моменту первого вступления мы определяем скорость фронта, и совершенно не интересуемся параметрами сигнала, который будет потом, после зарегистрированного момента первого вступления. И одна из моих лабораторных работ по курсу шахтной сейсморазведки как раз и представляла собой установку, в которой можно было определять скорость распространения фронта (V_фр) при изменении частоты излучающей пьезокерамики более чем в 10 раз (от 60 до 800 КГц). Смею уверить, что при столь широком диапазоне частот (а стало быть, и длин волн) зондирующего сигнала положение момента первого вступления на шкале времяизмерительного прибора оставалось неизменным.
     Но, с другой стороны, можно понять и тех, кто придумал этот запрет. Дело в том, что при определении скорости распространения фронта даже в идеальных по однородности средах (стекло, например), значение V_фр оказалось в значительной степени зависящим от геометрии измерительной установки. Зависимость экспериментально определяемой скорости распространения звука в однородных средах от условий измерения настолько непредставима, что ученым оказалось проще окружить эту проблему массой запретов, нежели разобраться в физике этого явления.

---

⁴ Поскольку скорость непосредственно не измеряется, а вычисляется в результате измерения временного интервала, то мы стараемся избегать понятия "измерения" скорости, а применяем термин "определение" скорости

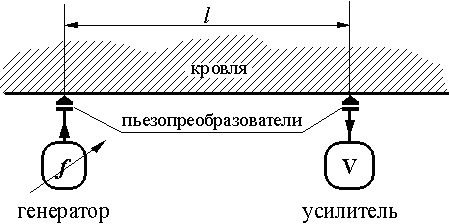
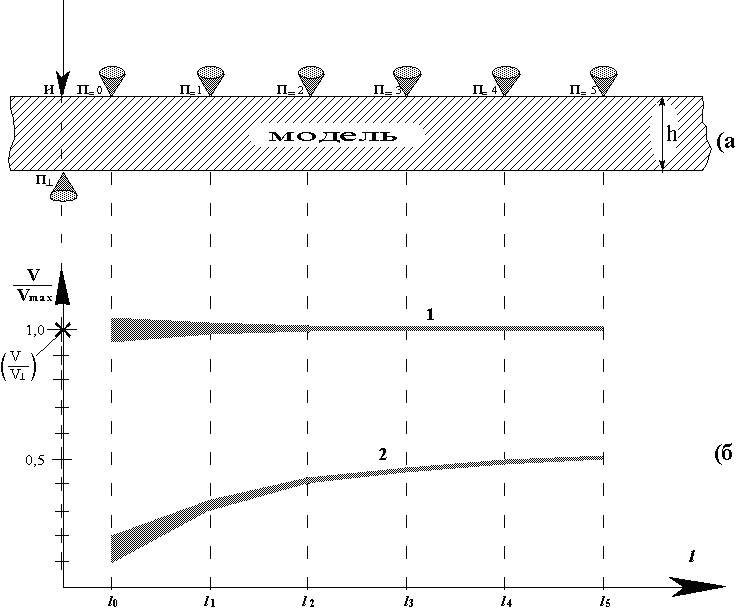
1.5.2. Описание измерений

     Схема лабораторной установки приведена на рис.1-5а. Исследуемая модель представляла собой лист оргстекла толщиной (h) 20 мм и размером 1,5Х1,5 м. Как излучатель И, так и приемники П находятся в середине листа, чтобы уйти от краевых эффектов.

Рис. 1-5

     Ударное воздействие в точке И осуществляется с помощью пьезокерамического преобразователя, возбуждаемого коротким электрическим импульсом. Регистрация моментов первого вступления осуществляется в нескольких точках для того, чтобы выяснить, во-первых, возможное наличие анизотропии, а во-вторых, возможную зависимость определяемой скорости от величины измерительной базы. Значок "" означает, что измерение осуществляется в направлении, перпендикулярном плоскостям модели; а значок "₌" - вдоль поверхности модели.
     Скорость V определяется как отношение l к t, где l - расстояние от точки И до соответствующего приемника, а t - время, необходимое для прохождения упругой волны расстояния l. Момент прохождения через точку контакта с соответствующим приемником определяется по моменту первого вступления. То есть речь идет об определении скорости распространения фронта упругой волны V_фр.
     Погрешность определения скорости V_фр с уменьшением измерительной базы l увеличивается в связи с увеличением относительных погрешностей как l, так и t за счет уменьшения их абсолютных значений. Это отражено утолщением линии графиков на рис.1-5б.
     Измерениям, выполненным на листе из оргстекла, соответствует график 1. Как видим, значения скорости распространения звука в этой плоскопараллельной структуре остаются постоянными и не зависящими от геометрии измерительной установки. То есть, на просвет скорость V_фр такая же, как и при распространении звука вдоль листа, независимо от l. Скорость эта в оргстекле примерно равна 3000 м/с.
     Такие результаты позволяют нам считать проведенные измерения правомерными.
     Однако при переходе от оргстекла к стеклу результаты измерений коренным образом изменяются. Первые же измерения, выполненные на листовом стекле, дали другие, и совершенно неожиданные результаты. Оказалось, что величина скорости V_фр не остается постоянной, а зависит от условий измерения. А именно, от геометрии измерительной установки. Результаты этих измерений отражены на рис.1-5б зависимостью 2.
     Наибольшее значение имеет величина V_фр, то есть скорость, выявленная путем сквозного прозвучивания стеклянного листа. Величина скорости V_фр оказалась примерно равной 6x10³ м/с. То есть на первом этапе, мы могли бы даже согласиться, что это есть скорость продольных волн. При профилировании вдоль поверхности этой модели, при наибольших значениях l величина V_фр= оказывается примерно вдвое меньшей, чем V_фр. Ну, здесь тоже можно было бы согласиться, что это скорость поперечных волн. Однако при уменьшении измерительной базы l величина V_фр= не остается постоянной, и не приближается к значению V_фр, как можно было бы ожидать, а уменьшается. В пределе, определяемом допустимой погрешностью (в пределах 20%), величина V_фр= уменьшается до 10³ м/с.
     На этом этапе, не будем пока выяснять причин получившихся результатов. Отметим только, что график, подобный зависимости 2 на рис.1-5б получается при исследовании плоскопараллельных структур из стекла, металлов и сплавов, керамики, цементных составов, горных пород, а также ледяного слоя замерзшего водоема.
     Естественно, что когда мы делали доклады о получающихся результатах, возникали сомнения в правомерности подобных измерений. Однако что касается правомерности проведенных измерений, то мы ее уже доказали при исследовании листа из оргстекла.
     И еще один момент. Малые значения скорости при небольших значениях измерительной базы при сейсморазведочных работах хорошо известны. Это истолковывается как следствие наличия приповерхностной зоны малых скоростей. Предполагается, что скорость распространения в приповерхностных породах имеет низкое значение в связи с их выветрелостью. Как видим, это не так. В объектах из стекла и металлов приповерхностных зон нет, но малые значения скорости V_фр при малых значениях измерительной базы все равно имеют место.
     Естественно, что сразу после получения таких результатов эта измерительная установка в качестве лабораторной для обучения студентов не могла применяться по причине полного непонимания тех результатов, которые были получены с ее помощью.

1.S. Выводы по разделу 1

     Испокон веков считалось, что законы распространения упругих колебаний в газообразных, жидких и твердых однородных средах в общих чертах подобны законам распространения света. Пуассон предположил, что твердые среды от жидких и газообразных отличаются тем, что в них, вследствие наличия сдвиговых деформаций распространяются кроме продольных еще и поперечные колебания. Но принципиально это ничего не изменило, так как предполагается, что эти и многие другие типы упругих колебаний все равно распространяются по законам геометрической оптики. А следовательно, в общем виде, свойства поля упругих колебаний и акустические сигналы, регистрируемые соответствующими приемниками, определяются интерференционными процессами.
     Содержание предыдущего абзаца, по сути, является основой всей современной парадигмы той части физики, которая ведает упругими колебаниями.
     Но вот оказалось, что в твердых средах в составе сейсмосигналов существуют затухающие гармонические колебания. То есть в твердых средах есть объекты, имеющие свойства колебательных систем.
     И сразу возникла очень серьезная проблема. Ведь если при ударном воздействии на горный массив происходит преобразование этого воздействия в гармонический процесс, то о распространении этого первичного импульса в пространстве земной толщи уже не может быть речи. Его просто нет. Мы ведь не можем рассматривать звучание, скажем, колокола как следствие многократного переотражения в нем первичного ударного воздействия. Колокол работает как объемный резонатор, и если приложить к его поверхности сейсмоприемник, то никаких следов первичного, ударного воздействия увидеть не удастся. Сейсмоприемник зафиксирует только собственные колебания объемного резонатора, которые имеют вид затухающей синусоиды.
     То есть обнаруженный эффект возникновения в земной толще гармонических затухающих колебаний поставил под сомнение всю общепринятую парадигму теории поля упругих колебаний. Ну, что ж, согласно основным принципам методологии развития научного познания, один несложный эксперимент вполне может оказаться могильщиком как угодно мощной и высоко математизированной теории. Однако на своем опыте могу сказать, что в жизни все происходит иначе…
     Особого внимания заслуживает описанный эксперимент по определению скорости распространения звука в пластинах. Эксперимент этот настолько прост, что может быть выполнен буквально в школьных условиях. Результаты его хорошо повторяемы. Но осуществление его находится под запретом. Ученые, в присутствии которых я проводил эти измерения в своей лаборатории, в представительных аудиториях это категорически отрицали. Более того, даже некоторые из моих бывших сотрудников, с которыми мы вместе задумывали и готовили эти измерения, заявляли потом, что никаких измерений не было. Ну, на мой характер, уже хотя бы в силу этих причин, следовало разобраться с физикой этих столь неугодных результатов...
     Если бы мы жили на Луне, и нам были бы чужды интересы конкретных людей, мы бы конечно предпочли экспериментально обоснованную парадигму, той, которая возникла умозрительно и ни одно положение которой экспериментами не подтверждается. Однако в реальности каждая существующая область знания связана с судьбами людей, и ожидать добровольного признания ошибочности какого-то научного направления нельзя. Ну, как можно требовать, чтобы, скажем, пожилые люди, имеющие научные степени и звания, признались даже сами себе, что вся их жизнь ушла на движение в тупиковом направлении и принесена в жертву научному заблуждению...