 |
| О нас | Услуги | Оборудование | Книги по теме | Примеры | Связь | Карта | Форум | Видео | En |
VI. ИЗУЧЕНИЕ СТРУКТУРЫ ПОЛЯ УПРУГИХ КОЛЕБАНИЙ В ЛАБОРАТОРНЫХ УСЛОВИЯХ
|
VI.2. Эффект акустического резонансного поглощения (АРП) Если бы собственные колебания слоев-резонаторов действительно шли на продольных волнах, то изучать этот процесс следовало бы с помощью эффекта монохроматора. Для того чтобы подойти к экспериментальным исследованиям, напомним некоторые моменты, связанные с этим эффектом.
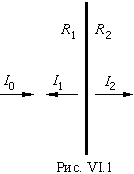
Поскольку I0=I1+I2 , то
где R = рV ; р - плотность среды; V - скорость распространения упругого процесса. Из выражения (VI.4) видно, что если по обе стороны от границы среды имеют одинаковое удельное акустическое сопротивление, то границы, с позиции акустических измерений, как бы и не существует.
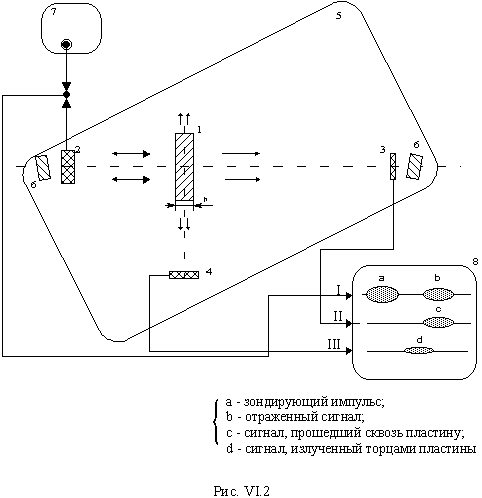
Совмещение оси измерительной установки с диагональю бассейна 5 и установка рассеивателей 6 – это все меры, направленные на уменьшение влияния отражений от стенок бассейна.
При снятии подобных зависимостей особый интерес представляют разного рода резонансные эффекты, и в частности, известный из литературы эффект монохроматора, аналогичным которому в оптике является эффект просветления. Этот эффект заключается в отсутствии отражения от пластины и полном через нее прохождении звукового потока. Эффект монохроматора (мх) должен наблюдаться при следующем условии: h = n где Vv - скорость объемных (продольных) волн;
То есть, если собственные колебания слоев-резонаторов действительно идут на продольных волнах, то выражение (VI.6) при n = 1 должно совпадать с выражением (VI.1).
Получив эффект монохроматора, мы совершенно случайно увидели еще один эффект.
Выражение (VI.7) вынесено в раздел I как (I.1).
|
VI.3. Поиск условий возникновения собственных упругих колебаний в плоскопараллельных структурах Как уже упоминалось неоднократно, современная теоретическая акустика категорически отрицает наличие каких бы то ни было собственных упругих колебательных процессов1. И это вполне естественно, поскольку интерференцией собственные упругие процессы не описываются, а других механизмов, по крайней мере, на мысленном, как бы теоретическом уровне, вроде бы, и нет. Однако приведенные выше эксперименты свидетельствуют о наличии собственных колебаний, и при этом даже обнаружен столь представительный свидетель существования резонансных явлений как эффект АРП.
1 Исключение составляют собственные изгибные колебания, которые возникают в тонких пластинах, пленках и оболочках. |
VI.4. О составных слоях - резонаторахПри прохождении упругих волн через несколько границ, не содержащих приграничных зон |
VI.5. Изучение влияния зон
|
VI.6. Изучение структуры поля упругих колебаний Из материала, помещенного в предыдущих параграфах, видно, что мы научились, наблюдая эффект монохроматора, выделять объемные волны. Наблюдая эффект АРП, мы подтвердили существование сдвиговых волн и, кроме того, выяснили, что именно на них происходят собственные упругие колебательные процессы. Но при этом оказалось, что свойства выявленных типов волн имеют отличия от свойств этих же волн, но описываемых общепринятой теоретической акустикой.
|
VI.7. Применение пьезопленочных и пьезокерамических аэп для изучения структуры поля упругих колебаний Мысль применить пьезопленку для аэп возникла в связи с попытками добиться широкополосности преобразователей за счет отсутствия в пленке, которая по механическим свойствам подобна полиэтиленовой, собственных колебаний.
Табл. VI.1.
Как видно из этой таблицы, пьезопленка как в режиме излучения, так и в режиме приема не намного уступает по эффективности пьезокерамике, но это касается тех случаев, когда пленка работает в паре с керамикой. В случае пары пленка-пленка коэффициент передачи оказывается столь малым, что полезный сигнал на выходе выделить на фоне помех не удается. В связи с этим у меня возникла гипотеза, состоящая в том, что пьезопленка излучает один тип упругих колебаний, а принимает другой, ортогональный излучаемому.
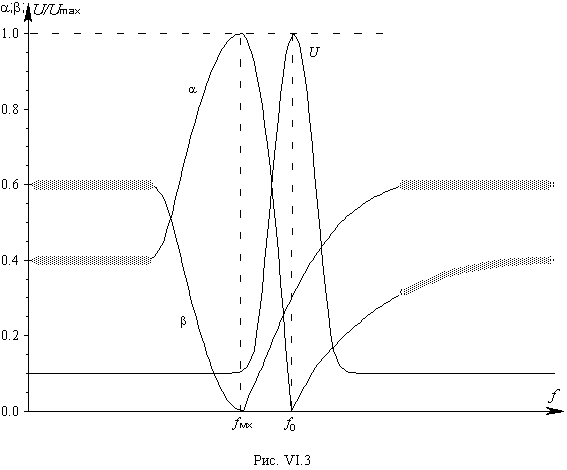
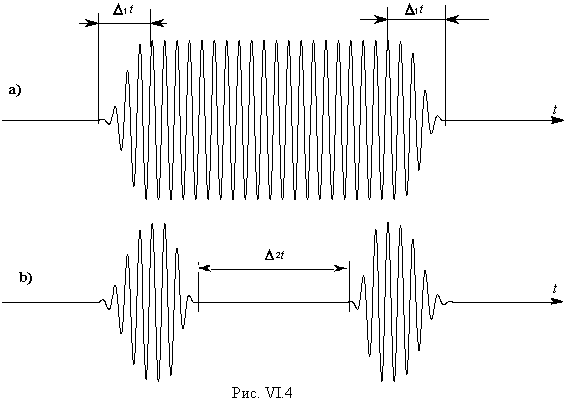
Подавая теперь на два входа двухканального осциллографа сигналы с этих двух пьезоэлементов, увидим на частоте f0 изображение, подобное приведенному на рис.VI.4. При этом с пьезопленки будет снят сигнал, подобный сигналу а, а с пьезокерамике - подобный сигналу б. Особенность наблюдаемых сигналов заключается в том, что при наблюдении эффекта АРП с помощью такого комбинированного аэп, при частоте зондирующего сигнала, равной собственной частоте прозвучиваемой пластины-резонатора f0 (то есть на резонансе), исчезает только тот сигнал (средняя часть его, как это показано на рис. VI.3), который снимается с пьезокерамики. Амплитуда же сигнала, снимаемого с пьезопленки, на изменение частоты вблизи прохождения через резонанс не реагирует.
Далее, с-составляющая при наличии соответствующих условий (при наличии слоя-резонатора) преобразуется в собственный колебательный процесс, который идет на сдвиговых волнах. Обозначим сдвиговые волны индексом sh (сдвиг - shear).
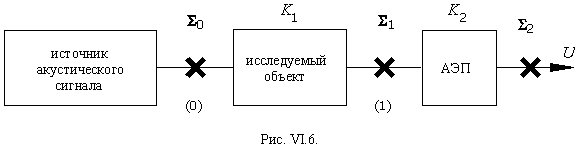
По мере прохождения акустического сигнала, обусловленного наличием источника, через исследуемый объект и через звукопроводящую часть аэп, структура поля упругих колебаний, определяемая соотношением между c и p-составляющими объемных волн, изменяется в зависимости от характера звукопроводности как исследуемого объекта, так и самого аэп.
Поле в точке 0 в точке 1 в точке 2 Коэффициент передачи акустического сигнала от источника до точки приложения аэп К1 определяется звукопроводностью исследуемого объекта:
В дальнейшем коэффициент передачи акустического сигнала будем называть звукопроводностью. Как видно из выражения (VI.8), звукопроводность является комплексной величиной, мнимая часть которой обращается в нуль при условии:
То есть когда на входе и на выходе звукопроводящего объекта не изменяется соотношение с и p-составляющих объемных волн. Это происходит тогда, когда материал объекта не содержит приповерхностных зон, обладающих реактивной звукопроводностью.
В случае применения пьезопленочного аэп величина электрического напряжения на его выходе U определяется величиной Рассматривая влияние звукопроводности аэп на характер поля в точке (2), можно понять причину искажений сигнала, описанных в параграфе V.1, при наличии у величины К2 мнимой составляющей.
При наличии мнимой составляющей звукопроводности аэп при использовании пьезокерамики возможны ситуации, когда |
VI.8. Об искусственном создании зон
|
N |
среда слоя h2 |
h2(мм) |
f0h (кГц) |
Vshслоя h2 (м/с) |
1 |
стекло |
4 |
400 |
3600 |
2 |
---//--- |
6 |
327 |
3594 |
3 |
оргстекло |
2 |
367 |
1497 |
4 |
---//--- |
4 |
246 |
1494 |
5 |
---//--- |
6 |
186 |
1505 |
6 |
---//--- |
8 |
149 |
1503 |
7 |
вода |
2 |
260 |
814 |
8 |
---//--- |
3 |
195 |
802 |
9 |
---//--- |
4 |
155 |
790 |
10 |
---//--- |
5 |
130 |
793 |
11 |
---//--- |
6 |
110 |
779 |
VI.9. Изучение влияния граничных условий на колебательные свойства пьезоэлементов Эксперимент состоит в таком же исследовании пьезокерамического диска, какое описано в параграфе II.3, с использованием схемы, приведенной на рис. II.16. Дополнение заключается в том, чтобы исследовать колебательные свойства этого пьезоэлемента при различных граничных условиях.
|
VI.10. О проблеме эхо - сигнала в сейсморазведке Сама идея создания сейсморазведки базируется на уверенности в наличии эхо-сигнала от залегающих в породной толще отражающих границ.
|
VI.11. Несколько замечаний о методах измерения скорости
|
Выводы по разделу VIСовместное рассмотрение приведенных в предыдущих разделах результатов экспериментов и их толкований позволяет объединить их в виде нескольких пунктов общих представлений о свойствах собственных упругих колебаний.
|
| Обсудить статью |
| При использовании материалов сайта ссылка на www.newgeophys.spb.ru обязательна | Публикации о нас |
|
|
|
|
|
 ß0 = I1 / I0 ;
ß0 = I1 / I0 ; 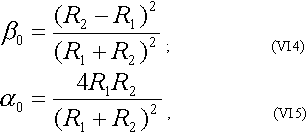
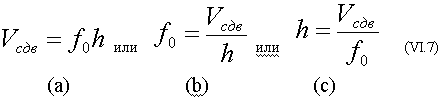

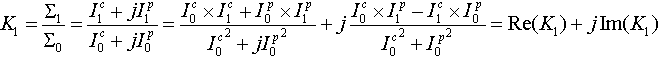 (VI.8)
(VI.8)
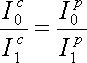 (VI.9)
(VI.9)
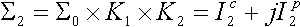 (VI.10)
(VI.10)
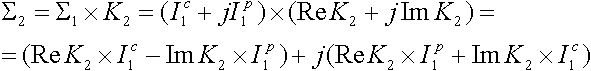 (VI.11)
(VI.11)
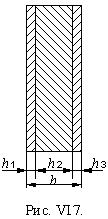 Исследованию будут подлежать трехслойные структуры, подобные показанной на рис. VI.7, в которых в середине (h2) находится слой из материала ряда оргстекла, а по краям (h1 и h3) - ряда стекла. Суммарная толщина пакета - h.
Исследованию будут подлежать трехслойные структуры, подобные показанной на рис. VI.7, в которых в середине (h2) находится слой из материала ряда оргстекла, а по краям (h1 и h3) - ряда стекла. Суммарная толщина пакета - h.
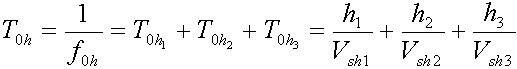 (VI.12)
(VI.12)
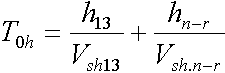 (VI.13)
(VI.13)
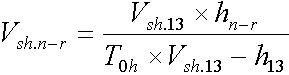 (VI.14)
(VI.14)
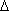 h.
h.