V. ИЗУЧЕНИЕ СОБСТВЕННЫХ
УПРУГИХ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ

     Собственные колебания - это реакция колебательных систем на импульсный (в общем случае, широкополосный) сигнал. Во всех областях физики собственные колебания проявляются совершенно одинаково. А именно, наличием в наблюдаемом сигнале гармонических затухающих процессов.
     Собственные колебания в электротехнике регистрируются при изучении электрических колебательных контуров. В механике - при изучении пружинных устройств, маятников. В акустике - при изучении камертонов, струн и прочих устройств, в которых участвуют изгибные колебания. Во всех этих случаях известны механизмы существования колебательных систем. Или, иначе говоря, механизмы преобразования импульсного воздействия в гармонический отклик. При распространении упругих колебаний в земной толще, а также в разного рода массивных объектах предполагалось, что собственные колебания отсутствуют, поскольку механизмы преобразования удара в гармонический сигнал были неизвестны.
     Предполагается, что как бы ни был сложен акустический (сейсмо) сигнал, он всегда может быть описан интерференцией между отдельными отражениями зондирующего импульса. В разделе II я (опираясь на мнение Фурье), как мог, доказывал, что интерференцией может быть описан любой процесс кроме гармонического.
     Однако анализ сейсмических и акустических сигналов неизбежно приводит к выводу о том, что собственные, имеющие гармонический характер, упругие колебательные процессы возникают практически при любых акустических и сейсмических измерениях повсеместно и независимо от нашего желания, а также вопреки ему.
     Рассмотрим некоторые случаи, когда можно зарегистрировать собственные колебательные процессы при сейсмо и акустических измерениях, а также методические подходы для изучения их.
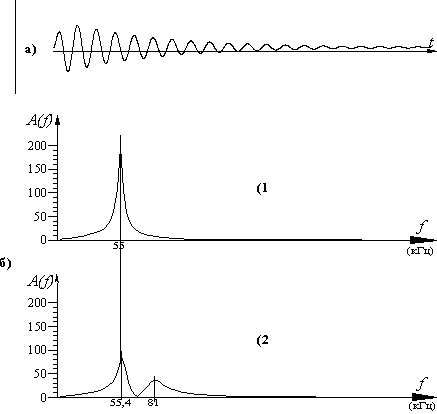
     Если нанести удар по поверхности Земли, то, используя в качестве акустоэлектрического преобразователя (аэп) сейсмоприемник любой из существующих систем, а в качестве регистратора - сейсмостанцию, увидим сейсмосигнал. В соответствии с известными и общепринятыми принципами акустики, сейсмосигнал должен представлять собой совокупность отражений зондирующего импульса, сформированного ударом, от всех имеющихся в земной толще отражающих границ. Однако на самом деле обнаружить в составе сейсмосигнала составляющие, обусловленные именно отражением импульсного воздействия от каких-то границ, не удастся. Обычно вид сейсмосигнала представляет собой не совокупность импульсов, как это обычно описывается в учебниках, а совокупность затухающих гармонических процессов. Причем амплитуда принимаемого сигнала многократно превышает ту, которая имела бы место при наблюдении отражений от каких бы то ни было геологических объектов. Длительность наблюдаемых сигналов описанного вида также очень велика и зависит от нижней границы частотного диапазона регистрирующей аппаратуры. При нижней границе частотного диапазона, составляющей десятки герц, эта длительность может достигать единиц секунд. При этом изменчивость очертаний сейсмосигнала очень велика, и вид его существенно изменяется при любых самых незначительных изменениях геометрии измерительной установки.
     Такой сейсмосигнал соответствует повседневной практике сейсморазведчиков. Неоправданные ничем большая амплитуда и длительность всем известны. Принято считать, что происходит это потому, что отражающих границ, залегающих в исследуемом горном массиве, бесчисленное множество, а сейсмосигнал есть результат интерференции между всеми элементарными отражениями, и поэтому может иметь любой внешний вид. Несколько противореча этому мнению, считают (и называют) длительно звучащие составляющие сейсмосигналов паразитным звоном, и основным направлением сейсморазведки последние 80 лет является подавление, уничтожение этого "звона".
     Для того, чтобы прийти к уверенности, что этот "паразитный звон" как раз и является "голосом" массива, содержащим информацию о его строении, оказалось необходимым прежде всего устранить искажения сейсмосигнала. То есть, добиться идентичности электрического сигнала, снимаемого с сейсмоприемника, с сейсмосигналом и избавиться от спектральных искажений, вносимых схемой обработки сейсмосигнала, а также провести серию сейсмоизмерений в условиях, где имеется достаточно надежная геологическая информация о строении массива.
     Что касается требования идентичности сигналов на входе и выходе сейсмоприемников, то не может не вызвать удивления то, что за всю историю сейсморазведки ни у кого этот вопрос не возник. А вместе с тем, схема первичной проверки на идентичность сигналов элементарно проста. Если на поверхность сейсмоприемника (сп) с высоты 30-50 см уронить стальной шарик диаметром не более 2 мм, то при отсутствии искажений сейсмоприемником электрический сигнал, снимаемый с него, должен иметь вид единичного короткого импульса плюс 2-3 таких же импульса, но гораздо меньшей амплитуды, возникших за счет отражений внутри сп первичного импульса. Однако на практике дело обстоит совершенно иначе. Если подобному испытанию подвергнуть любой из существующих в Мире сп, то электрический сигнал будет иметь вид длительного колебательного процесса. Исключение составляет сп, специально созданные для спектрально-сейсморазведочных измерений [14].
     Как показал опыт, информация, содержащаяся в предыдущем абзаце, вызывает серьезные возражения. Дело в том, что изложенный там подход очень противоречит сложившемуся мнению. Так, согласно многочисленной научной и учебной литературе считается, если спектр собственных колебаний сейсмоприемника является существенно более высокочастотным, чем спектр исследуемых колебательных процессов, то такой сп следует считать абсолютно широкополосным и не вносящим спектральные искажения. На самом деле, это не так, и наличие собственной колебательности у сп на любой частоте приводит к спектральным искажениям во всем частотном диапазоне. Подробнее этот момент будет рассмотрен далее.
     Требованию достаточной геологической изученности отвечают угольные шахты, и поэтому именно там проводились основные наши натурные исследования с помощью специально созданной для этого, лишенной собственной колебательности, аппаратуры.
     Первое же измерение в кровлю угольной шахты (в 1977 г) показало наличие в сейсмосигнале гармонического сигнала с частотой 1 кГц. Измерение это осуществлялось в очистном забое, вблизи разведочной скважины, и поэтому было известно, что в кровле, непосредственно над угольным пластом залегал слой весьма прочного песчаника мощностью (толщиной) 2,5 м. Думаю, что любой на моем месте попытался бы связать эти две величины. Я предположил тогда, что мощность песчаника может оказаться равной половине длины упругой волны:

h = 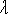 / 2 = V / (2f), и тогда V = 5000 м/с.

     Такое значение вполне может иметь скорость продольных волн в песчанике. Я сразу понял, что если эта зависимость мною угадана правильно, то таким образом можно будет в дальнейшем без бурения определять мощность непосредственной кровли (то есть породного слоя, залегающего непосредственно над угольным пластом). Информация эта крайне важна для того, чтобы прогнозировать устойчивость кровли. Единственное серьезное сомнение заключалось в том, что, согласно справочникам, скорость продольных волн даже у одной и той же породы может иметь очень различные значения, а уж у различных пород кровли, и тем более.
     Велико же было мое удивление, когда при следующем измерении, когда в кровле залегал аргиллит 4-метровой мощности, частота гармонического сигнала в сейсмосигнале имела величину 625 Гц. То есть, опять получалось, что значение скорости, при котором выполняется приведенное выше соотношение, равно 5000 м/с.
     Как ни удивительно, но дальнейшие измерения на самых различных горных породах показали удивительное постоянство этой скорости. Несовпадение не превышало ± 10%. Это настолько противоречило существующим взглядам, что я даже докладывать об этом не мог. Ни на конференциях, ни даже заказчику. Вышел я из сложившегося положения следующим образом.
     Я предложил использовать для определения мощности породных слоев с помощью спектрально-акустических измерений следующее выражение:

h = K / f ,      (V.1)

где K – коэффициент, имеющий размерность скорости и равный 2500.
     На рис. V.1а приведен один из сейсмосигналов, полученный при исследовании кровли подземной выработки угольной шахты вблизи от точки, где была разведочная скважина.
     На рис. V.1б дан спектр этого сигнала. При этом ось плотности спектра A(f) горизонтальна, а вертикально приведены две оси – ось частот в герцах и ось глубин, в метрах. Пересчет оси частот в ось глубин осуществлен с помощью выражения (V.1).
     Как видим, получается хорошее совпадение между местонахождением экстремумов на спектрограмме б и границами на разрезе в. Однако количество экстремумов на спектрограмме отличается от количества границ между литотипами, выявленных разведочным бурением. Так, непонятно происхождение двух экстремумов на глубинах 2 и 3 м. Экстремумы, соответствующие этим границам, настолько четкие, что о случайности не может быть и речи. Мы заметили, что довольно часто на малых глубинах, недалеко от угольного пласта встречаются экстремумы, не подтверждаемые бурением.
     С другой стороны, отсутствует экстремум на глубине 12, 5 м, там, где бурением выявлено изменение литотипа.
     Так или иначе, наряду с множеством совпадений при шахтных измерениях возникало множество вопросов и сомнений.
     Для проверки универсальности эмпирически выявленного соотношения (V.1) было необходимо осуществить измерение на простейшем объекте, каковой являлась бы единичная плоскопараллельная структура. Таким объектом при некоторых условиях может служить слой льда на поверхности замерзшего водоема.

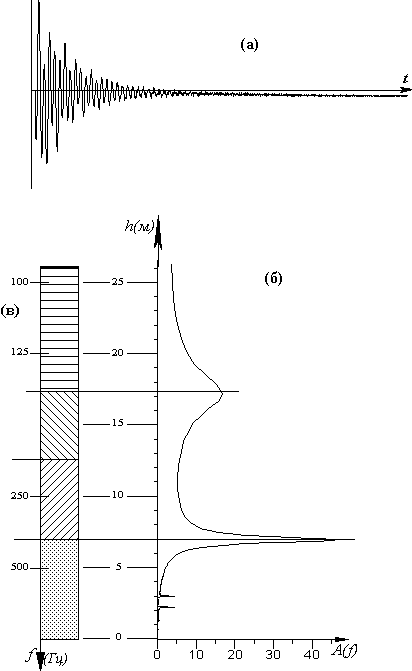
Рис. V.1

     Отклик на ударное воздействие слоя льда при работе зимой на одном из озер под Санкт-Петербургом оказался идентичным сигналу, показанному на рис. II.2б. Измерения повторялись несколько раз в течение зимы, и изменяющаяся при этом толщина льда вполне соответствовала выражению (V.1) при K 2000 м/с. Эти измерения позволяют утверждать, что плоскопараллельная структура может проявлять свойства одночастотной колебательной системы.
     Для того чтобы установить, от чего зависят значения K, необходимо осуществить подобные измерения на различных объектах при тщательном контроле за составом материала и геометрией объектов. Однако при лабораторных акустических измерениях сложность выявления отдельных источников гармонических затухающих процессов возрастает многократно. Прежде всего, возникает проблема источника возбуждающего сигнала. Использование механических источников (удар, взрыв) оказывается далеко не всегда возможным, так как произвольно задать длительность ударного взаимодействия _у нельзя, а вместе с тем, требования к ее величине определяются, исходя из выражения (II.8), размерами исследуемого объекта. То есть, чем меньше исследуемый объект, тем меньше должна быть величина _у, что обеспечить далеко не всегда возможно. А, кроме того, в исследуемых в лабораторных условиях объектах зачастую возникают при использовании механических источников изгибные колебания, наличие которых еще более увеличивает сложность наблюдения подлежащих изучению процессов.
     Использование электроакустических излучателей (эап) также имеет свою специфику в связи с тем, что при импульсном возбуждении излучаемый ими акустический импульс обязательно содержит их собственный колебательный процесс, то есть представляет собой гармонический затухающий процесс с удароподобным началом.
     Попробуем во всех этих сложностях разобраться, двигаясь от простого к сложному.
     При импульсном механическом воздействии на объект реакция предположительно представляет собой сумму, составляющие которой:

• а) совокупность отражений этого воздействия от границ объекта;
• б) совокупность гармонических затухающих процессов. В пределе, гармонический затухающий процесс может быть и единичным;
• в) совокупность отражений от границ объекта гармонических затухающих процессов, возникших в результате ударного на объект воздействия.

     Совершенно необязательно, чтобы реакция на удар содержала все три составляющие. Умение расчленять сейсмосигнал и анализировать отдельно его составные части необходимо для эффективного использования поля упругих колебаний.
     В современной теоретической акустике отражения зондирующего воздействия от границ (эхо-сигналы) собственным процессом не считается. Это чисто терминологический момент, мы не будем его оспаривать, и тоже под собственными процессами будем понимать только те, которые имеют вид гармонических затухающих сигналов. Напомним только еще раз, что эхо-сигнал, в отличие от собственных процессов, по форме должен совпадать с зондирующим импульсом.
     Начнем с исследования простейших объектов, то есть, имеющих один-единственный собственный размер. Один из таких объектов - сплошной шар из однородной изотропной среды диаметром D, а другой - бесконечно протяженная плоскопараллельная структура толщиной (мощностью) h.

V.1. Стеклянный шар

     Сплошной шар является объектом, имеющим один размер. Кроме того, шар не имеет собственных изгибных процессов. Выбрали мы стекло в качестве материала шара, потому что трудно себе представить более однородный материал. Но вместе с тем, единичным, ни с чем не связанным объектом шар быть не может. Он либо лежит на чем-то, либо на чем-то висит, и при ударном его возбуждении необходимо учитывать неизбежно возникающую реакцию опоры на удар. Реакцию эту можно ослабить, одновременно и подвесив шар, и положив его так, чтобы распределить нагрузки между двумя опорами примерно поровну, а также используя в качестве акустической изоляции поролон.
     Диаметр имеющегося в наличии стеклянного шара D=55 мм; воздействие механическое, возникающее в результате падения на поверхность шара стального шарика диаметром 2 мм с высоты 300 мм.
     На рис.V.2 показаны временные (а) и спектральные (б) изображения сигналов, полученные с помощью пьезопленочного (1) и пьезокерамического (2) аэп. Сигнал 1 имеет вид единичного гармонического затухающего процесса с параметрами: f₀₁=55 кГц; добротность A(55кГц)=197.

Рис. V.2

     Наличие реакции на удар в виде единичного затухающего гармонического сигнала (сигнал 1) однозначно свидетельствует о том, что стеклянный шар является одночастотной колебательной системой. При этом видим наглядно: единственный размер - единственный собственный колебательный процесс. Коэффициент пропорциональности K между диаметром шара и собственной его частотой равен 3025 м/с.
     Сигнал 2 - двухчастотен. Кроме основного, присущего шару колебательного процесса, на частоте 81 кГц виден еще один, обусловленный наличием собственного колебательного процесса самого пьезокерамического преобразователя. Этот пример также является типичным. Подобная картина имеет место тогда, когда колебательный процесс изучают с помощью регистратора, имеющего собственную колебательность.
     Но не только это различие наблюдается между сигналами 1 и 2. Отличаются и параметры основного процесса. Частота основного процесса, зарегистрированного пьезокерамическим аэп, оказалась на 0,4 кГц выше, чем зарегистрированного пьезопленкой (f₀₂=55,4кГц), а добротность - ниже (A(55,4 кГц)=87). Различие значений частот собственных колебаний при использовании различных аэп свидетельствует о том, что какой-то из применявшихся аэп вносит частотные искажения.
     Наблюдаемый уход частоты на 0,4 кГц составляет меньше 1% от основной частоты, и, казалось бы, в этом нет ничего страшного. Но специальные измерения в шахтных условиях показали, что при использовании сейсмоприемника, имеющего собственные частоты, уход частоты может быть практически любым, а главное, меняющимся от измерения к измерению. Физика этого явления будет рассмотрена в параграфе VI.5.
     Отметим, что в составе сигнала, полученного в результате наблюдения реакции стеклянного шара на удар, не видна информация об отражении зондирующего сигнала от стенок шара. То есть, если эта составляющая сигнала даже и существует, то она имеет амплитуду, во много раз меньшую, чем собственные колебания.

V.2. Исследование собственных колебательных процессов плоскопараллельных структур

     Плоскопараллельные структуры занимают особое место в этой работе по следующим причинам. Во-первых, осадочный чехол Земли - этот главный объект нашего внимания -  представляет собой совокупность более или менее выдержанных по мощности плоскопараллельных геологических структур. Во-вторых, очень многие объекты искусственного происхождения также представляют собой совокупность слоев. А в-третьих, к слоистой структуре можно привести множество объектов, исследование которых с помощью поля упругих колебаний может представить интерес.

V.2.1. Общие представления о моделировании

     При натурных исследованиях не представляется возможным знать досконально геометрию исследуемого объекта (ведь вполне может оказаться, что нижняя поверхность предположительно плоскопараллельного ледяного слоя не является плоскостью), а также варьировать какими бы то ни было качествами слоя-резонатора с тем, чтобы получить информацию о влиянии их на его колебательные свойства. Для получения этой информации на достаточно метрологически корректном уровне оказалось необходимым разработать методику лабораторных исследований, применять физическое моделирование и, в частности, с использованием пьезоэлементов.
     Моделирование тех или иных процессов применяют тогда, когда непосредственное изучение их не представляется возможным или, по каким-то причинам, целесообразным.
     Классическим примером моделирования является испытание уменьшенных моделей самолетов в аэродинамической трубе. Этот классический пример представляет собой физическое моделирование. Здесь исследуемый объект отличается от реального лишь размерами, а воздействие на объект идентично реальному. Физическому моделированию обычно присуще понятие масштабного коэффициента. В данном случае масштабный коэффициент определяется соотношением между размерами реального самолета и его модели, и этим коэффициентом определяется соотношение между воздействием воздушного потока на модель в аэродинамической трубе и воздействием встречного воздуха на самолет в полете.
     В тех случаях, когда физическое моделирование по каким-то причинам неприменимо, можно использовать моделирование математическое. Оно заключается в том, что с помощью вычислительной техники решаются системы уравнений, описывающих поведение исследуемого объекта. Исходным моментом при этом должно быть совпадение результатов решения уравнений для какого-то конкретного и уже известного состояния объекта. Тогда, задавая изменения аргументов и граничных условий, можно надежно описать и другие его состояния. Эффективность математического моделирования тем выше, чем полнее наша информация о реальном поведении исследуемого объекта или процесса. Иначе говоря, чем надежнее метрологическое обеспечение при экспериментальном выявлении значений аргументов используемого уравнения и его граничных условий.
     Возможности вычислительной техники не безграничны, и к тому же далеко не всегда существуют возможности аналитического описания тех или иных явлений. В этих случаях иногда удается применить методы аналогового моделирования, которое заключается в следующем.
     Допустим, нам необходимо осуществить исследование некоторых тепловых процессов. При этом непосредственное измерение температуры внутри объекта далеко не всегда возможно, и, следовательно, физическое моделирование исключается. Законы распределения температурных градиентов известны, но аналитическое их описание чрезвычайно сложно и громоздко. На помощь может прийти тот факт, что распространение тепла описывается теми же уравнениями, что и распространение электромагнитного поля. Поэтому распространение тепла можно изучать, регистрируя распространение электрического тока в электрической схеме при условии соответствия электрических параметров схемы-модели тепловым параметрам изучаемого объекта.
     Аналоговое моделирование широко используется при изучении разного рода механизмов. Это осуществляется с помощью специально разработанных электромеханических аналогий.
     Различные виды моделирования - физическое, математическое и аналоговое - имеют один общий момент, который заключается в том, что моделировать можно только уже известные явления. Независимо от вида моделирования, в результате его осуществления неизбежно возникает некоторая побочная информация, не имеющая отношения к изучаемому явлению. Для эффективного исследования методом моделирования необходимо заранее знать, какого рода информация является основной с тем, чтобы на всю остальную, выходящую за ее рамки, просто не обращать внимания.
     Отсюда следует вывод о том, что с помощью моделирования в принципе невозможно получение какой-то неожиданной информации, какого-то нового знания. Все неожиданное и новое будет неизбежно уничтожено при обработке результатов моделирования. То есть, получается, что с помощью моделирования нельзя сделать открытия какого-то неизвестного эффекта. Мы, может быть, даже увидим этот эффект, но отбросим его, потому что примем его за издержки моделирования. Таким образом, назначение моделирования - изучение и уточнение уже имеющейся информации о том или ином явлении, но не получение новой.
     Так, в аэродинамической трубе неоднократно возникали вибрации моделей, однако до тех пор, пока вибрация не стала причиной гибели настоящих самолетов, это явление при моделировании не изучалось, потому что предполагалось, что в реальности оно возникнуть не может.
     Знание особенностей и принципиальных возможностей моделирования оказалось особенно необходимым при изучении законов формирования и распространения поля упругих колебаний. Мы не будем еще раз останавливаться на причинах, не позволяющих применять при изучении акустики математическое и аналоговое моделирование, но оказалось, что и с физическим моделированием дело обстоит также совсем неоднозначно.
     Исследование можно считать моделированием, если масштабный коэффициент отличен от единицы. То есть, при акустическом физическом моделировании в соответствии с выбранным коэффициентом должен быть изменен основной акустический параметр - скорость распространения упругих волн. А это, как известно, невозможно, и, стало быть, понятие масштабного коэффициента при акустических измерениях просто лишено смысла.
     Следовательно, физическое моделирование акустических процессов в полном смысле этого понятия неосуществимо, а всяческие исследования уменьшенных (или увеличенных) моделей является не моделированием, а полноценным акустическим исследованием.
     Поэтому проводя акустические измерения на пьезоэлементах, которые можно рассматривать как модели плоскопараллельных структур, мы вместе с тем не занимаемся физическим моделированием в полном смысле этого слова. Смысл моделирования у нас заключается в том, что при изучении акустических свойств геологических структур в лаборатории проводятся измерения на объектах, по каким-то параметрам похожих. Отсюда возникает ряд как ограничений, так и преимуществ. Преимущества заключаются в том, что никакая получаемая при этом исследовании информация не является побочной, и мы не потеряем ее, сколь бы неожиданной она ни оказалась. Именно так оно и произошло, когда, изучая на пьезомодели уже известный из литературы эффект монохроматора, мы случайно обнаружили совершенно еще неизвестный эффект акустического резонансного поглощения (АРП), подробное описание которого будет дано в разделе VI.
     Ограничения же при акустическом моделировании определяются возможностями при изготовлении тех или иных моделей. Так, представляется совершенно невыполнимым в лабораторных условиях создание модели бесконечно протяженной плоскопараллельной структуры, создание условий, когда при механическом ударном возбуждении слоя-резонатора отсутствуют изгибные колебания, обычно не наблюдаемые при измерениях в горном массиве в естественном его залегании. Есть при лабораторных измерениях еще и другие ограничения, о которых будем рассказывать в процессе дальнейшего повествования.

V.2.2. Использование пьезоэлементов для изучения собственных колебательных процессов

     Первым примером такого использования пьезокерамики можно считать рассмотренный в параграфе II.3 способ определения собственной колебательности пьезоэлементов с помощью схемы, изображенной на рис. II.16. Но прежде, чем продолжить подобные исследования, необходимо решить один принципиальный вопрос.
     Колебательные свойства пьезоэлементов известны давно. Это, в первую очередь, кварцевые резонаторы, применяемые во всем Мире уже больше 80 лет. Кроме них нынче широко применяются в радиопромышленности пьезокерамические резонаторы. Резонансные свойства пьезоэлементов объясняются в существующей на сегодняшний день научной литературе исключительно наличием пьезоэффекта. Принято считать, что пьезорезонаторы эквивалентны колебательным контурам, в силу чего и обладают резонансными свойствами, и теория этих резонансных устройств организована таким образом, что, опираясь на теорию контуров, не имеет никаких точек соприкосновения с теорией поля упругих колебаний.
     В отличие от этого, общепринятого подхода, мы считаем, что наличие резонансных свойств пьезорезонаторов определяется исключительно акустическими свойствами материала объекта, его геометрией и качеством границ. Пьезоэффект же является лишь средством для получения информации о наличии этих резонансных свойств. Для того, чтобы разобраться в этом противоречии, проведем исследования на двух совершенно идентичных пьезокерамических дисках из титаната бария.
     Для проведения этого эксперимента используем установку для определения скорости распространения упругих колебаний сквозь пластины, изображенную на рис. III.3. Установим в ней два одинаковых пьезокерамических диска таким образом, чтобы один из них находился на месте образца 4, а другой - симметрично ему относительно излучателя 1. При этом обе эти пьезокерамические пластины должны быть строго параллельными друг другу, а также пьезопреобразователям измерительной установки, и тогда можно будет добиться, чтобы оба сигнала, снимаемые с пьезоприемников 2 и 3, и подаваемые на два входа двухканального осциллографа, оказались идентичными.
     Уточним. В отсутствии исследуемых пьезопластин сигналы, поступающие на оба входа осциллографа, обязательно должны быть идентичными. Это является признаком нормального функционирования измерительной установки. Помещаемые в установку исследуемые нами пьезопластины полностью изменяют очертания сигналов, но идентичность их должна сохраняться. Это будет признаком одинаковости исследуемых пластин. Спектр этих сигналов будет определяться суммой резонансных свойств прозвучиваемых пластин и пьезопреобразователей измерительной установки.
     Теперь следует одну из прозвучиваемых пластин лишить пьезосвойств, для чего достаточно нагреть ее до температуры, превышающей точку Кюри, и повторить прозвучивание. При этом мы убедимся, что форма сигнала, снимаемого с пьезопластины 2 или 3 никак не изменяется в зависимости от того, обладает прозвучиваемая пластина пьезосвойствами или нет.
     Таким образом, можем считать доказанным, что резонансные свойства пьезоэлементов не зависят от наличия у них пьезосвойств, а целиком определяются акустическими свойствами материала. Наличие же пьезосвойств, как уже говорилось, может позволить эти акустические свойства обнаруживать и изучать.
     На основании доказанного можем считать правомерным осуществление физического моделирования для изучения собственных колебательных процессов в объектах с использованием пьезосвойств материала этих объектов.
     Воспользовавшись схемой, изображенной на рис. II.16, подвергнем испытаниям имеющиеся в наличии пьезокерамические диски. Результаты этих испытаний сведены в таблицу V.1.

     Значения скоростей V_h и V_d, которые определяются перемножением каждого размера объекта на соответствующую собственную частоту (см. выражение (I.1), могут быть определены с очень высокой степенью точности. Это то, к чему мы всегда стремились. Но теперь, когда эта точность достигнута, оказалось, что скорость V в керамике различается в различных направлениях. Что это? Следствие какой-то анизотропии? Принято считать, что пьезокерамика обладает анизотропией, обусловленной ее электрической поляризацией. Однако если сравнить отношение скоростей (V_h / V_d) в различных строках таблицы, то увидим, что оно стремится к единице при стремлении к единице отношения h/d. И, в конце концов, что же это за скорость, которая определяется произведением размера объекта на соответствующую ему собственную частоту?
     Проведя аналогичные измерения на множестве пьезокерамических пластин с размерами 3,5*99 мм, мы зафиксировали разброс значений (V_h / V_d) до 15%. Означает ли это, что испытывавшиеся пластины имеют различные механические свойства (размеры их строго одинаковые) или нарушенность? Чтобы ответить на эти вопросы, необходимо провести подобные исследования на металлических объектах, для которых возможно чередовать акустические измерения с разного рода нагружениями, а также осуществлять контроль развивающейся в результате нагружений нарушенности другими, неакустическими способами. Однако металлы не обладают пьезоэффектом, и для их исследования нужно применять другие методы акустических измерений. В частности, методы спектрально-акустической дефектоскопии.
     С помощью моделирования на пьезоэлементах можно проследить влияние на колебательные свойства резонатора граничных условий, что будет сделано в разделе VI.

V.2.3. Использование ультразвукового прозвучивания для регистрации косвенных признаков наличия собственных колебательных процессов

     Воспользовавшись установкой, изображенной на рис. III.3, убедимся вначале, что при импульсном возбуждении излучателя 1 и отсутствии образцов оба сигнала, снимаемые с аэп 2 и 3, совершенно идентичны. С помощью двухканального осциллографа в этом можно убедиться, совместив оба сигнала.
     Если в качестве прозвучиваемого образца 4 взять пластину из оргстекла, то сигнал, снимаемый с аэп 3, уменьшится только по амплитуде. То есть если, увеличив коэффициент усиления соответствующего канала осциллографа, уравнять сигналы по амплитуде, то сигналы опять окажутся идентичными и полностью совпадут друг с другом.
     Совершенно другая будет картина, если в качестве прозвучиваемого образца взять пластину из другого материала. Например, стеклянную. Возбуждаемый в такой пластине зондирующим импульсом типа изображенного на рис. II.20б собственный колебательный процесс в отдельности увидеть не удастся. Увидим же мы при этом только изменение очертаний сигнала. Сигнал станет существенно длительнее, и огибающая его будет изменяться при изменении толщины прозвучиваемой пластины-резонатора.
     То есть признаком наличия в прозвучиваемой пластине собственного колебательного процесса (резонансных свойств) является изменение очертаний зондирующего сигнала при прохождении его через эту пластину.
     Прозвучиваемая пластина при этом должна быть строго параллельной преобразователям (случай нормального прозвучивания). При непараллельности прозвучиваемой пластины преобразователям наличие в ней собственных колебательных процессов проявляется иначе.
     Но прежде чем показать это отличие, необходимо обратить внимание на исключительность объектов из оргстекла. В разделе III мы выделили исключительность этого материала при проведении измерений, направленных на определение скорости распространения фронта упругих колебаний. И вот, с другой стороны, этот материал оказывается исключительным и при наблюдении собственных упругих колебательных процессов. Будем в связи с этим разделять исследуемые пластины на пластины-нерезонаторы (оргстекло) и на пластины-резонаторы (стекло, керамика, металлы и сплавы, горные породы и т.п., по этому признаку). То есть, опять же, ряд стекла.
     При медленном и плавном повороте образца вокруг собственной оси в том случае, если образец - пластина-нерезонатор, изображения сигналов, снимаемых с преобразователей 2 и 3, будут идентичными друг другу независимо от угла поворота ф (изменение соотношения амплитуд между ними не в счет). В том же случае, если образец - пластина-резонатор, очертания обоих этих сигналов станут идентичными только при значении угла ф, равном или большем значения ф_кр.
     Кроме этого, еще один косвенный признак наличия собственных колебательных процессов может быть установлен при наблюдении закономерностей, касающихся затухания поля при распространении его вдоль слоев-резонаторов.

V.2.4. Затухание поля при распространении его вдоль слоев-резонаторов

     Затухание поля при распространении его вдоль плоскопараллельных структур так, как это показано в разделе IV, происходит только в слоях-нерезонаторах. В слоях же резонаторах картина принципиально иная. В этом нетрудно убедиться с помощью простейших акустических измерений, и в частности, с помощью установки, схема которой показана на рис. III.1а.
     На рис. V.3 показаны зависимости амплитуды сигнала от величины измерительной базы l, полученные с помощью этой установки.

Рис. V.3

     График а соответствует исследованиям на оргстекле, а б - на пластинах из материалов ряда стекла.
     Источник ударного воздействия представляет собой устройство, с помощью которого маленький стальной шарик может падать на исследуемую пластину с одной и той же высоты, и в одну и ту же точку. Размеры исследуемой плоскопараллельной структуры должны быть такими, чтобы, работая примерно в середине ее, иметь расстояние от преобразователя до ближайшего края пластины существенно бóльшим, чем l_max. Это необходимо для того, чтобы отраженный от края пластины сигнал оказался разделенным с сигналом, возникающим в результате ударного воздействия.
     Разница в затухании при измерениях поочередно в пластине-резонаторе и в пластине-нерезонаторе очень ощутима. Напомним, что распространяющийся вдоль пластины-нерезонатора сигнал по очертаниям эквивалентен исходному, возникающему при падении шарика. В слое-резонаторе амплитуда сигнала при увеличении l уменьшается незначительно, сам же сигнал имеет очень большую длительность, и по очертаниям не имеет ничего общего с сигналом, наблюдаемом при исследовании слоя-нерезонатора, поскольку распространяется вдоль слоя-резонатора не исходный сигнал, а вызванный им собственный колебательный процесс слоя-резонатора.
     Результаты по своему характеру не изменятся, если вместо падающего шарика использовать в качестве излучателя возбуждаемую коротким электрическим импульсом пьезокерамику.
     Затухание поля при распространении в слое-резонаторе при r > h столь незначительно, что становится понятной физика одного используемого испокон веков эффекта.
     Речь о том, что, приложив ухо к земле, можно услышать топот лошадей значительно раньше, чем их увидеть. Но одно здесь необходимо отметить. Мы при этом слышим не сам топот, а возбуждаемые им собственные упругие колебания, распространяющиеся вдоль породных слоев-резонаторов. С учетом этого становится понятным, почему топот конницы слышен в виде звонкого низкочастотного гула: это соответствует распространению собственного звучания вдоль совокупности слоев резонаторов большой мощности.
     Надо сказать, что если не учитывать наличие собственного колебательного процесса в стеклянном слое-резонаторе, то столь существенная разница в затухании и длительности сигналов, получаемых при исследовании стекла и оргстекла необъяснима.
     Обратим теперь внимание на положительный экстремум на зависимости (б). На расстоянии от излучателя, примерно равном толщине пластины-резонатора, имеется участок, в пределах которого сигнал с увеличением l не уменьшается, а, наоборот, вопреки ожиданию, увеличивается.
     Наличие зон, в которых наблюдается увеличение сейсмосигнала при удалении от источника, сейсморазведчикам известно, но объясняется это исключительно интерференцией, и в научной литературе, если не ошибаюсь, не упоминается. Дело в том, что согласно общепринятым подходам, изменение величины акустического (сейсмического) сигнала трактуется как показатель изменения энергии этого сигнала. Увеличение же энергии поля упругих колебаний с удалением от его источника безусловно невозможно, так как противоречит закону сохранению энергии. С другой стороны, это подтверждает, что, как показано в разделе II.4, судить об энергии по величине электрического напряжения на клеммах сейсмоприемника нельзя.
     К сожалению, я не получил разрешение на публикацию результатов, полученных в Геофизическом институте СО АН РФ при проведении эксперимента, который, на мой взгляд, подтверждает факт крайне низкого затухания собственных колебаний в породных слоях-резонаторах.

Выводы по разделу V

     Задача настоящего раздела - дать экспериментальные доказательства того, что сигнал при акустических измерениях в большинстве твердых сред представляет собой один или несколько гармонических колебательных процессов. Из этого следует, что исследуемые с помощью поля упругих колебаний объекты содержат одну или несколько колебательных систем.
     В разделе II.7 было высказано предположение о том, что поскольку, с одной стороны, собственные колебания обусловлены процессами, описываемыми на мнимой оси, а с другой, поскольку на мнимой оси должны описываться поперечные волны, то, во-первых, упругие собственные колебания формируются поперечными волнами, а во-вторых, их распространение должно характеризоваться крайне низким затуханием. График б на рис.V.3 это подтверждает.