 |
| О нас | Услуги | Оборудование | Книги по теме | Примеры | Связь | Карта | Форум | Видео | En |
III. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛЯ УПРУГИХ КОЛЕБАНИЙСкорость распространения упругих волн является единственной характеристикой поля упругих колебания, которая может быть определена экспериментально на метрологически удовлетворительном уровне. Это породило множество направлений, в которых кинематические характеристики поля упругих колебаний используют для получения информации о различных акустических, механических и прочностных параметрах металлов и сплавов, горных пород, разного рода бетонных конструкций и тому подобных объектов. При этом многие общепринятые способы определения кинематических характеристик поля упругих колебаний не являются бесспорными, и задача настоящего раздела - проанализировать их с метрологических позиций. |
III.1. Скорость распространения фронта упругих колебаний Прежде всего, необходимо отметить, что скорость не может быть измерена непосредственно, а определяется в результате соответствующей математической обработки непосредственно измеряемых величин. А отсюда следует то, что достоверность и погрешность определяемой скорости зависит от погрешности и правильности трактовки измеряемых величин.
Получаемая при этом величина V соответствует скорости, усредненной по величине 1 Постоянство скорости распространения упругих колебаний в однородных по вещественному составу средах в силу своей очевидности является фундаментальным положением теоретической акустики. |
III.2. Первая попытка измерения скорости продольных волн В соответствии с общепринятыми представлениями, продольные волны присутствуют практически во всех случаях распространения звука и являются самым быстрым упругим процессом. Следовательно, представляется логичным определять скорость распространения продольных волн, выявляя самую быструю часть процесса. Информацию же о скорости распространения самой быстрой части процесса можно получить, определяя скорость фронта волны Vфр, которую как раз и измеряют путем регистрации момента первого вступления. То есть момента времени, разделяющего состояния наличия и отсутствия сигнала.
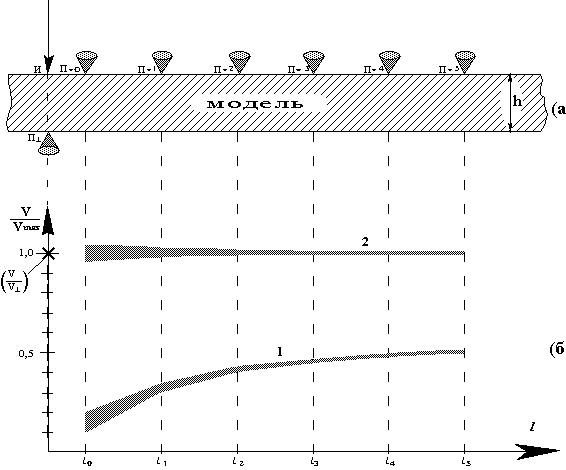
Схема измерительной установки приведена на рис. III.1а. Ударное воздействие осуществляется с помощью пьезокерамического преобразователя, возбуждаемого коротким электрическим импульсом. Регистрация моментов первого вступления осуществляется в нескольких точках для того, чтобы выяснить, во-первых, возможное наличие анизотропии, а во-вторых, возможную зависимость определяемой скорости от величины измерительной базы. Значок " Регистрируя же момент первого вступления, мы совершенно не интересуемся всеми теми колебательными процессами, которые, возможно, последуют за ним. Вполне может быть, что эти колебательные процессы действительно будут характеризоваться какими-то частотами и, соответственно, длинами волн, но к определению скорости распространения фронта Vфр они не имеют никакого отношения.
2 Здесь и далее, кроме особо оговоренных случаев, мы будем иметь в виду акустику твердых сред. |
III.2.1. Замечание о дисперсии Воспользовавшись предложенной логикой, проведем ревизию еще одного кажущегося очевидным, и в силу этого укоренившегося положения. Я имею в виду дисперсию. Дисперсия, то есть зависимость скорости распространения волнового процесса от его частоты, предлагается как одна из причин экспериментально регистрируемого непостоянства формы сигнала и непостоянства скорости распространения упругих колебаний.
|
III.3. Вторая попытка измерения скорости продольных волн О том, в чем состоит различие акустических свойствах в двух видах материалов (ряда стекла и ряда оргстекла), речь пойдет в следующих разделах, а пока что мы проверим известное предположение, заключающееся в том, что величина Vфр
График а показывает зависимость Vфр
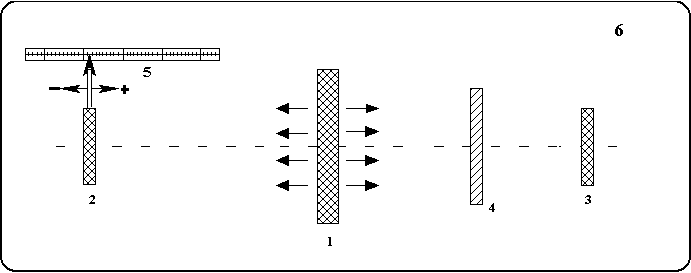
Непосредственно измерение заключается в том, чтобы перемещать пьезоприемник 2 до положения, при котором на экране двухканального осциллографа наблюдается совпадение моментов первого вступления, регистрируемых приемниками 2 и 3. В случае отсутствия исследуемой пластины 4 это условие выполняется при одинаковых расстояниях этих приемников от излучателя.
где
Vфр.max. – это величина скорости распространения скорости фронта, к которой стремится измеряемая величина скорости Vфр.ср. при увеличении толщины пластины.
3 Измерения скорости Vфр |
III.4. Понятия фазовой и групповой скорости Отсутствие экспериментального подтверждения постоянства скорости распространения упругих колебаний в однородных изотропных средах очень смущало ученых в течение всего периода существования акустики. Однако настоящий ученый свое смущение никогда не покажет, а сделает вид, что так и быть должно. И именно для этого было привлечено в акустику понятий групповой и фазовой скорости. Чтобы судить о правомерности применения этих понятий в акустике, коснемся истории их возникновения.
|
III.5. Об отношении к непостоянству скорости фронта внутри однородных сред С самого начала формирования взглядов на физику поля упругих колебаний, которое можно отнести к XVIII веку, возникла, как само собою разумеющееся, уверенность в том, что скорость распространения упругих колебаний в пределах однородных монолитных материалов есть величина постоянная. Мне не удалось нигде найти ни малейших следов каких-либо сомнений по этому поводу. Как результат этой уверенности, скорость распространения упругих волн попала в волновое уравнение в виде постоянного коэффициента.
|
III.6. Исследование механических свойств зон
|
III.7. О связях между скоростью упругих колебаний, механическим напряжением и прочностными характеристиками веществаИнформации о скорости различных типов упругих волн придается очень большое значение, поскольку, в соответствии с теорией упругости, значения Vпр и Vсдв имеют однозначную связь с модулями упругости:
где Е - модуль Юнга; G - модуль сдвига; v – коэффициент Пуассона; р - плотность среды, или, с другой стороны:
Однако при использовании этих выражений необходимо учесть два момента.
То есть погрешность определения модулей упругости многократно превышает погрешности определения скоростей, и выражения (III.6) и (III.7) приобретают практическое значение лишь в связи с разработкой новых высокоточных способов определения скоростей продольных и поперечных волн [11, 12]. Методы определения этих скоростей будут рассмотрены в разделе VI.
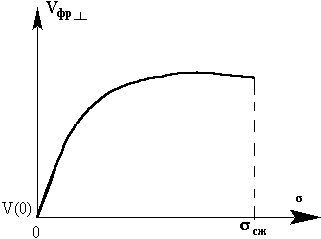
Рост скорости на начальном участке интерпретируется как следствие увеличения механического напряжения при отсутствии разрушений и остаточных деформаций. При этом увеличение скорости в образцах из некоторых пород может достигать 100% и более. Пологий участок зависимости при дальнейшем увеличении
При раздавливании образцов из горных пород под прессом разрушение их начинается с периферийных областей. Это подтверждает то, что изменения скорости в периферийных областях образцов после первых циклов нагружения следует истолковывать как следствие изменения нарушенности материала образцов. Изменения Vфр. кр при неизменности Vфр. ц после кратковременного незначительного нагружения образцов из горных пород свидетельствует о том, что даже при столь незначительных нагружениях (5-10% от |
III.8. О причинах влияния трещиноватости на скорость фронта С точки зрения традиционной теоретической акустики, наличие сомкнутых трещин в однородном по вещественному составу материале не должно оказывать воздействия на скорость распространения упругих колебаний. В самом деле, если скорость фронта в пределах однородного материала постоянна, то при переходе через сомкнутые трещины эта скорость изменяться не будет. Кроме того, акустическая граница - это место изменения удельной акустической жесткости, которая определяется как произведение скорости звука на плотность среды. Следовательно, сомкнутые трещины в принципе не являются границами для поля упругих колебаний. Через раскрытые же трещины поле упругих колебаний вообще не пройдет, и, следовательно, наличие и концентрация раскрытых трещин должны влиять лишь на затухание звука, но не на скорость его распространения.
|
ВЫВОДЫ по разделу III
|
| Обсудить статью |
| При использовании материалов сайта ссылка на www.newgeophys.spb.ru обязательна | Публикации о нас |
|
|
|
|
|
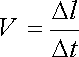 (III.1)
(III.1)
 , то есть скорость, выявленная путем сквозного прозвучивания модели. Величина скорости Vфр
, то есть скорость, выявленная путем сквозного прозвучивания модели. Величина скорости Vфр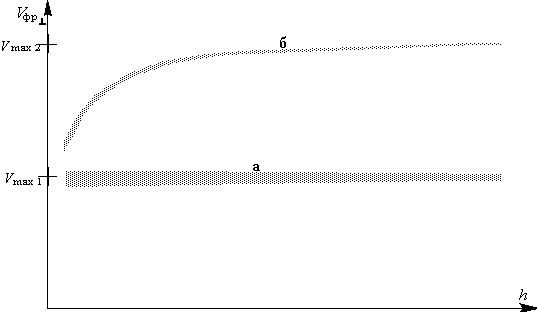
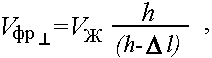 (III.3)
(III.3)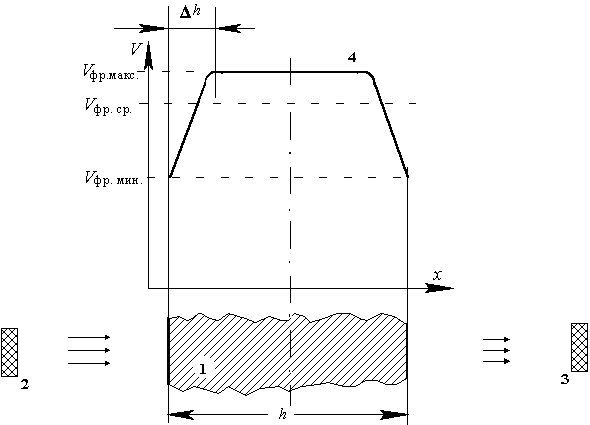
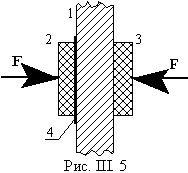 Шлифованные поверхности пластины 1 и преобразователей 2 и 3 притирают друг к другу с жидкой смазкой. Затем наблюдают местонахождение на экране осциллографа момент первого вступления, а также изменение его местонахождения на оси времени в зависимости от силы F прижима преобразователей. При этом в отсутствии прижима скорость Vфр.ср. окажется равной значению, приведенному зависимостью а на рис. III.2, а при увеличении силы прижима величина ее будет возрастать, достигая значения Vфр.max.
Шлифованные поверхности пластины 1 и преобразователей 2 и 3 притирают друг к другу с жидкой смазкой. Затем наблюдают местонахождение на экране осциллографа момент первого вступления, а также изменение его местонахождения на оси времени в зависимости от силы F прижима преобразователей. При этом в отсутствии прижима скорость Vфр.ср. окажется равной значению, приведенному зависимостью а на рис. III.2, а при увеличении силы прижима величина ее будет возрастать, достигая значения Vфр.max.
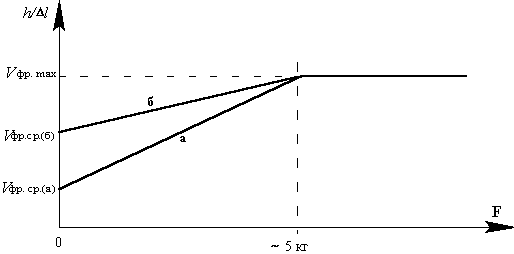
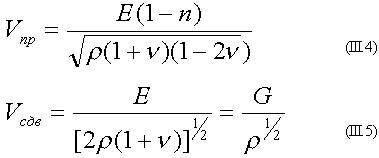
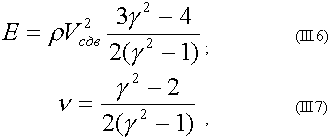
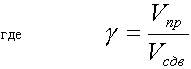

 В отличие от измерений, на основании которых обычно получают зависимости Vфр
В отличие от измерений, на основании которых обычно получают зависимости Vфр